Question

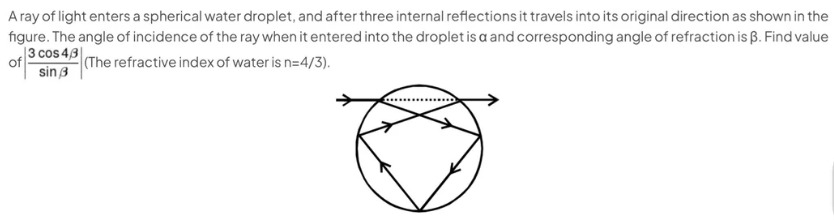
A ray of light enters a spherical water droplet, and after three internal reflections it travels into its original direction as shown in the figure. The angle of incidence of the ray when it entered into the droplet is $\alpha$ and corresponding angle of refraction is $\beta$. Find value of $\left|\frac{3 \cos 4 \beta}{\sin \beta}\right|$ (The refractive index of water is n=4/3).

Answer 1

4

Answer 2

The ray enters the droplet with angle of incidence $\alpha$ and angle of refraction $\beta$. After three internal reflections, it exits in the original direction. The total deviation of the ray is the sum of deviations at each refraction and reflection. The deviation at the first refraction is $\alpha - \beta$. The deviation at each internal reflection is $180^\circ - 2\beta$. The deviation at the final refraction is $\alpha - \beta$. The total deviation is $2(\alpha - \beta) + 3(180^\circ - 2\beta)$. Since the ray exits in the original direction, the total deviation is $0^\circ$. Thus, $2(\alpha - \beta) + 3(180^\circ - 2\beta) = 0$, which simplifies to $\alpha = 4\beta - 270^\circ$. Using Snell's law at entry, $\sin \alpha = n \sin \beta$. Substituting the expression for $\alpha$, we get $\sin(4\beta - 270^\circ) = n \sin \beta$. Using trigonometric identity $\sin(x - 270^\circ) = \cos x$, we have $\cos(4\beta) = n \sin \beta$. We are given $n = 4/3$, so $\cos(4\beta) = \frac{4}{3} \sin \beta$. We need to find the value of $\left|\frac{3 \cos 4 \beta}{\sin \beta}\right|$. Substituting the relation, we get $\left|\frac{3 (\frac{4}{3} \sin \beta)}{\sin \beta}\right| = |4| = 4$.