Question

A ray of light coming from the point $\left( {1,2} \right)$ is reflected at a point A on the $x -$axis and then passes through the point $\left( {5,3} \right)$. The coordinates of point A are:
(A) $\left( {\dfrac{{13}}{5},0} \right)$
(B) $\left( {\dfrac{{15}}{3},0} \right)$
(C) $\left( { - 7,0} \right)$
(D) None of these

Answer 1

The ray is coming from point $\left( {1,2} \right)$ and passing through $\left( {5,3} \right)$ after reflection at A. Draw a rough diagram to analyze the situation. Since the two points from which the ray is passing through are given, find the equation of the ray and then find the point where it is cutting the $x -$ axis.

Complete step by step answer:
According to the question, it is given that a ray of light is coming from point $\left( {1,2} \right)$ and while reflecting at point A on $x -$axis, it is passing through point $\left( {5,3} \right)$.
From this, we can say that the ray is passing through two points $\left( {1,2} \right)$ and $\left( {5,3} \right)$ and it is cutting $x -$ axis in the middle of these two points.
But if we draw a rough diagram of this (shown below), we can see that a ray of light passing through the points $\left( {1,2} \right)$ and $\left( {5,3} \right)$ can never cut the $x -$axis in the middle of these two points. Thus the information given in the question is ambiguous. And (D) is the correct option.

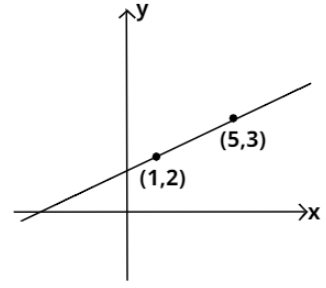
But if we have to find the point where the ray is cutting the $x -$axis, we can do so by finding its equation.
We have a formula of find the equation of a line i.e. $\left( {y - {y_1}} \right) = \dfrac{{\left( {{y_2} - {y_1}} \right)}}{{\left( {{x_2} - {x_1}} \right)}}\left( {x - {x_1}} \right)$.
Taking $\left( {1,2} \right)$ as $\left( {{x_1},{y_1}} \right)$ and $\left( {5,3} \right)$ as $\left( {{x_2},{y_2}} \right)$, the equation will be:
$\Rightarrow \left( {y - 2} \right) = \dfrac{{\left( {3 - 2} \right)}}{{\left( {5 - 1} \right)}}\left( {x - 1} \right) \\\ \Rightarrow \left( {y - 2} \right) = \dfrac{1}{4}\left( {x - 1} \right) \\\ \Rightarrow 4y - 8 = x - 1 \\\ \Rightarrow x - 4y + 7 = 0 \\\$
For the point where it is cutting $x -$axis, we’ll put $y = 0$, so we have:
$\Rightarrow x - 4\left( 0 \right) + 7 = 0 \\\ \Rightarrow x = - 7 \\\$
So the point where the ray is cutting $x -$axis is $\left( { - 7,0} \right)$ but its not point A as discussed above

So, the correct answer is Option C.

Note: There are other methods also to find the equation of a straight line. Some of them are shown below:
(1) If x and y intercepts of a line are known to us, we can easily determine the equation of line. Let $a$ and $b$ are the x and y intercepts respectively of the line, then the equation of line is:
$\Rightarrow \dfrac{x}{a} + \dfrac{y}{b} = 1$
(2) And if only y intercept is known along with the slope of line then also its equation can be easily determined. If $m$ is the slope and $c$ is the y intercept of the line, then the equation of line is:
$\Rightarrow y = mx + c$