Question

A ray light $AO$ in vacuum is incident on a glass slab at angle ${60^ \circ }$ and reflected at angle ${30^ \circ }$ along $OB$ as shown in the figure. The optical path length of light ray from $A$ to $B$ is:

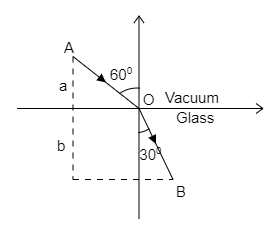
(A) $2a + 2b$
(B) $2a + \dfrac{{2b}}{3}$
(C) $\dfrac{{2\sqrt 3 }}{a} + 2b$
(D) $2a + \dfrac{{2b}}{{\sqrt 3 }}$

Answer 1

Hint The optical path length of light ray from $A$ to $B$ is determined by first using Snell’s law and then by using the optical path formula the optical path length is determined. By using Snell's law, the refractive index is determined, then the optical path formula is used.

Useful formula
The Snell’s law is given as,
${\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}$
Where, ${\mu _1}$ is the refractive index of the first medium, ${\theta _1}$ is the angle of the incidence, ${\mu _2}$ is the refractive index of the second medium and ${\theta _2}$ is the angle of the reflection.

Complete step by step solution
Given that,
The angle of incidence is given as, ${\theta _1} = {60^ \circ }$
The angle of reflection is given as, ${\theta _2} = {30^ \circ }$
Now,
The Snell’s law is given as,
${\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}$
By substituting the refractive index of the first medium, angle of the incidence and the angle of the reflection in the above equation, then the above equation is written as,
$1 \times \sin {60^ \circ } = {\mu _2}\sin {30^ \circ }$
From the trigonometry, the value of $\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2}$ and the value of the $\sin {30^ \circ } = \dfrac{1}{2}$, then the above equation is written as,
$1 \times \dfrac{{\sqrt 3 }}{2} = {\mu _2} \times \dfrac{1}{2}$
By rearranging the terms in the above equation, then the above equation is written as,
$2 \times \dfrac{{\sqrt 3 }}{2} = {\mu _2}$
By cancelling the same terms in the above equation, then the above equation is written as,
$\mu = \sqrt 3$
Now, the optical path formula is given as,
$\Rightarrow AO + \mu \left( {OB} \right)$
The above equation is also written as,
$\Rightarrow \dfrac{a}{{\cos {{60}^ \circ }}} + \sqrt 3 \dfrac{b}{{\cos {{30}^ \circ }}}$
From the trigonometry, the value of $\cos {60^ \circ } = \dfrac{1}{2}$ and the value of the $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$, then the above equation is written as,
$\Rightarrow \dfrac{a}{{\left( {\dfrac{1}{2}} \right)}} + \sqrt 3 \dfrac{b}{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}$
By rearranging the terms in the above equation, then the above equation is written as,
$\Rightarrow 2a + \sqrt 3 \dfrac{{2b}}{{\sqrt 3 }}$
By cancelling the same terms in the above equation, then the above equation is written as,
$\Rightarrow 2a + 2b$

Hence, the option (a) is the correct answer.

Note The ratio of the angle of the incident to the angle of the reflection is equal to the ratio of the refractive index of the two mediums. It is the statement which is given by Snell's law, when the problem is about the angle of the incident and the angle of reflection of the two mediums, Snell’s law will definitely play a major role. .