Question

A ray is incident on surface $AB$ of prism whose surface $BC$ is silvered at bottom as shown. The ray retraces its path after reflection from $BC$. If $r_1$ is zero then angle of prism is ($AB = AC$)

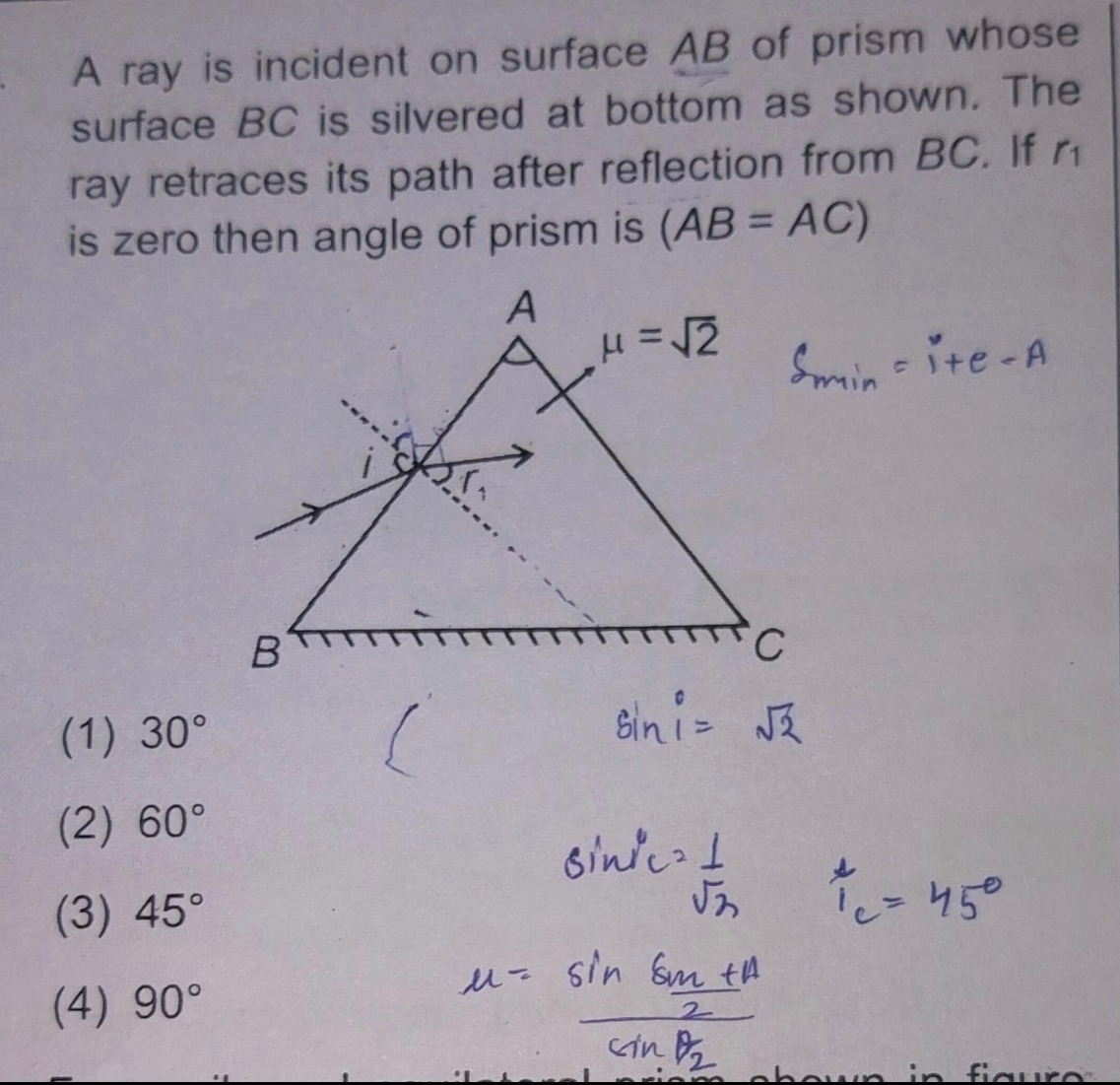
• A. $30^\circ$
• B. $60^\circ$
• C. $45^\circ$
• D. $90^\circ$

Answer 1

Answer: (B)

60^\circ

Answer 2

The problem states that a ray is incident on surface AB of a prism, and the angle of refraction at AB, $r_1$, is zero. This means the ray enters the prism normally to the surface AB. So, the incident ray is perpendicular to AB, and the refracted ray inside the prism travels along the normal to AB.

Let the ray inside the prism travel from point P on AB to point Q on BC. Since $r_1=0$, the ray PQ is along the normal to AB at P. The surface BC is silvered, and the ray retraces its path after reflection from BC. This implies that the ray incident on the silvered surface BC is perpendicular to BC. So, the ray PQ is perpendicular to BC. Let's assume the ray inside the prism is perpendicular to BC. This implies $r_2 = 0$.

Given $r_1 = 0$. $A = r_1 + r_2 = 0 + 0 = 0$.

So, if the ray exits normally, then $i'=0$, which implies $B = r_2$. We have $A = r_1 + r_2$. Given $r_1 = 0$, so $A = r_2$. Thus, $A = r_2 = B$. In $\triangle ABC$, $A + B + C = 180^\circ$. Given AB = AC, so $B = C$. $A + B + B = 180^\circ$. $A + 2B = 180^\circ$. Since $A = B$, we have $A + 2A = 180^\circ$. $3A = 180^\circ$. $A = 60^\circ$.