Question

A ray incident at $15{}^\circ$ on a refracting surface of a prism of angle $60{}^\circ$, suffers a deviation of$55{}^\circ$. The angle of emergence is:
A. $95{}^\circ$
B. $45{}^\circ$
C. $30{}^\circ$
D. $100{}^\circ$

Answer 1

You could recall the relation for angle of emergence in terms of the incident angle, prism angle and the angle of deviation. Or else, you could derive the same using simple geometry. Then you could directly substitute the given values from the question and hence get the answer easily.

Formula used: Relation connecting angle of incidence, angle of prism and angle of deviation with the angle of emergence,
$i+e-A=D$

Complete step by step answer:
In the question, we are given the incident angle of a ray that is incident on a refracting surface of prism whose prism angle is $60{}^\circ$ as$15{}^\circ$. This ray is known to suffer a deviation of $55{}^\circ$ and in that case, we are asked to find the angle of emergence.
In order to solve this problem let us find a relation connecting the given quantities with the angle of emergence.

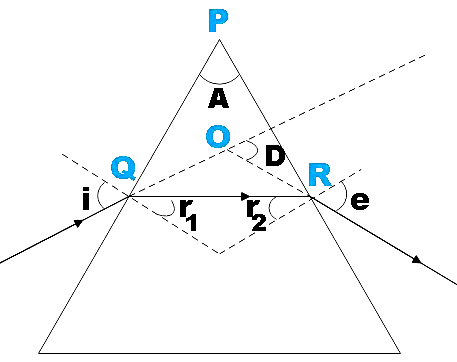
Consider triangle PQR, by angle sum property,
$A+\angle PQR+\angle QRP=180{}^\circ$
$\Rightarrow A+\left( 90-{{r}_{1}} \right)+\left( 90-{{r}_{2}} \right)=180{}^\circ$
$\therefore A={{r}_{1}}+{{r}_{2}}$ ………………………………… (1)
Now by exterior angle property of triangle OQR, we have,
$\angle OQR+\angle ORQ=D$
$\Rightarrow \left( i-{{r}_{1}} \right)+\left( e-{{r}_{2}} \right)=D$
$\Rightarrow i+e-\left( {{r}_{1}}+{{r}_{2}} \right)=D$
From (1),
$\therefore i+e-A=D$
Where, $i$ is the angle of incidence, e is the angle of emergence, A is the angle of prism and D is the angle of deviation.
Now that we have derived the required relation, we could directly substitute the values.
Given values from the question:
$i=15{}^\circ$
$A=60{}^\circ$
$D=55{}^\circ$
$15{}^\circ +e-60{}^\circ =55{}^\circ$
$\Rightarrow 15{}^\circ +e=115{}^\circ$
$\therefore e=100{}^\circ$

So, the correct answer is “Option D”.

Note: As we keep on increasing the incident angle, the angle of deviation decreases along with it. This is when the angle of minimum deviation comes into picture. This is the angle at which the deviation is minimum. For the case of minimum deviation of a prism the refracted ray is always found to be parallel to its base.