Question

A ray gets successively reflection from two mirrors inclined at an angle of ${40^o}$. If the angle of incidence for the first mirror is ${30^o}$, then net deviation of this ray after two reflections:
A) ${40^o}$
B) ${280^o}$
C) ${180^o}$
D) ${240^o}$

Answer 1

We can easily solve the question by using laws of reflection. We know that the angle of incidence equals the angle of reflection. Also, we can use the relation between the angle deviation and the angle of incidence. using these two relations we can easily find the answer to the given question.

Complete step-By-Step Answer:

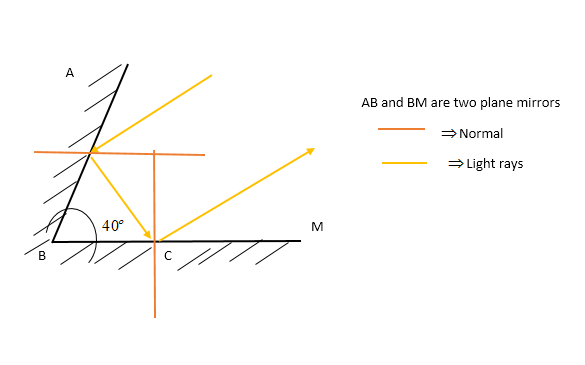
It is given in the question that:
The angle between the two mirrors $= {40^o}$
The angle of incidence on the first mirror $= {30^o}$
We know the laws of reflection states that when a light is reflected off a surface, angle of incidence equals angle of reflection.
Let $\angle i$ be the angle of incidence and$\angle r$ be the angle of reflection.
Thus, $\angle i = \angle r$
The angle of reflection in the first mirror $= {30^o}$
Thus, angle of deviation denoted by ${\delta _1}$ is $= \pi - 2 \times \angle i$
$\Rightarrow {180^o} - {60^o}$
${\delta _1} = {120^o}$
We also know, from the laws of reflection, the angle of reflection, the angle of incidence and the normal together sums up to${180^o}$.
The normal makes right angles with the plane of the mirror.
Now, considering triangle ABC in the diagram:
$\angle BAC = {90^o} - {30^o} = {60^o}$Since the normal makes right angles with the plane of the mirror.
$\angle ABC = {40^o}$(GIVEN)
Using the angle sum property we, obtain:
$\angle ACB = {80^o}$
Normal of the second mirror also makes right angle with the plane of the mirror, thus, $\angle ACD = {90^o} - {80^o} = {10^o}$
This is the angle of incidence and it equals angle of reflection for the second mirror.
Thus angle of deviation in mirror 2 is given by:
${\delta _2} = \pi - 2{i_2}$
Where, ${i_2}$ represents the angle of incidence for the second mirror.
${\delta _2} = {180^o} - {20^o} = {160^o}$
Therefore, total angle of deviation is given by:
$\delta = {\delta _1} + {\delta _2}$
$\Rightarrow \delta = {120^o} + {160^o} = {280^o}$
This is our required solution.

Thus, option (B) is correct.

Note: Angle of deviation, as we know, is defined as the angle between the straight line path and the reflected ray, which is equal to twice the angle of deviation.
Image formed by the plane mirror is virtual, erect and of the same size as that of the object.