Question
Question: A ray falls on a prism ABC (AB=AC) and travels as shown in the figure. The minimum refractive index ...
A ray falls on a prism ABC (AB=AC) and travels as shown in the figure. The minimum refractive index of the prism material should be
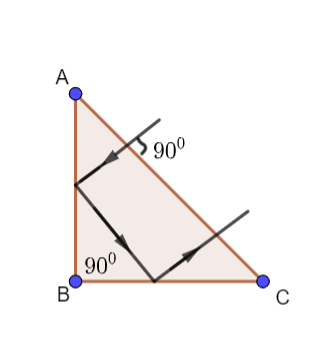
A. 34
B. 2
C. 1.5
D. 3
Solution
This question involves the use of modified form of Snell’s law given as μ1sinθ1=μ2sinθ2=...........=μnsinθn where μi is the refractive index of the ith material and sinθi is the sine of angle of incidence on the ith material. We will first identify the two surfaces where refraction is taking place. Then we will apply the modified form of Snell’s law and make proper substitutions. We will take μair=1 .
Complete step by step solution:
The refractive index of a material is the ability of the material to bend a ray of light entering through an interface towards or away from the normal.
This is mathematically given as the ratio of sine of angle of incidence to the sine of angle of refraction.
A more commonly used form is the below mentioned mathematical expression.
μ1sinθ1=μ2sinθ2=...........=μnsinθn
Here μi is the refractive index of the ith material and sinθi is the sine of angle of incidence on the ith material.
This is a modified form of the Snell’s law
Now let us understand the sequence of paths followed by the light ray.
First the light ray is incident on the surface AC from outside the prism at an angle 900 . Since, it enters along the normal it does not undergo any refraction. This light ray is now incident on the surface AB and gets reflected. It is now incident on the surface BC from which it gets reflected.
The diagram would be
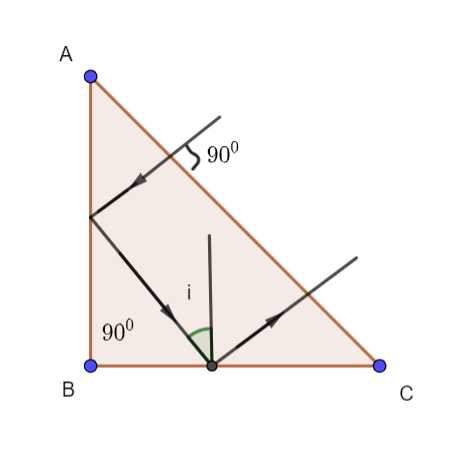
The light ray would follow the laws of reflection which state that the angle of incidence would be equal to the angle of reflection. Here, the sum of both these angles is 900 . So, we can say that
2∠i=900
∠i=450
Now, this light ray is incident on the surface AC from inside the prism with the angle of incidence equal to 450 .
Applying the modified form of the Snell’s law, we have
μairsin900=μprismsin450
We know that μair=1 .
Making proper substitutions, we have
1=μprism×21
⇒μprism=2
Note: We apply Snell’s law only where refraction is taking place. The reflecting surfaces have a different relationship between the angle of incidence and the angle of reflection. The minimum refractive index condition is satisfied on its own here since we have already chosen the maximum value of angle of incidence which is 900 .
