Question

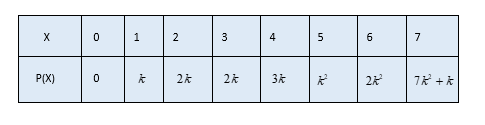
A random variable X has the following probability distribution:
Determine
(i) $k$
(ii) $P(X < 3)$
(iii) $P(X > 6)$
(iv) $P(0 < X < 3)$

Answer 1

Hint: In this question we will use the concept of probability distribution of a random variable. The probability distribution of random variable X is defined only when we have the various values of the random variable e.g. ${x_1},{x_2},{x_3},.......,{x_n}$together with respective probabilities ${p_1},{p_2},......,{p_n}$ satisfying $\sum\limits_{i = 1}^n {{p_i} = 1}$

Complete step-by-step answer:
(i) we know that the sum of all probabilities in a probability distribution is always unity. Therefore,
$\Rightarrow P(X = 0) + P(X = 1) + P(X = 2) + ............. + P(X = 7) = 1 \\\ \Rightarrow 0 + k + 2k + 2k + 3k + {k^2} + 2{k^2} + 7{k^2} + k = 1 \\\ \Rightarrow 9k + 10{k^2} = 1 \\\ \Rightarrow 10{k^2} + 9k - 1 = 0 \\\$
Now, after solving this equation, we get
$\Rightarrow (10k - 1)(k + 1) = 0$.
$\Rightarrow 10k - 1 = 0$ or $k + 1 = 0$
$\Rightarrow 10k = 1 \\\ \Rightarrow k = \dfrac{1}{{10}} \\\$ or $k = - 1$.
Hence, k = -1 cannot be possible because probability can’t be negative.
Therefore , $k = \dfrac{1}{{10}}$.
(ii) $P(X < 3)$.
$\Rightarrow$ $P(X < 3)$= $P(X = 0) + P(X = 1) + P(X = 2)$.
$\Rightarrow$ $P(X < 3)$= $0 + k + 2k$
$\Rightarrow$ $P(X < 3)$= 3k
putting $k = \dfrac{1}{{10}}$, we get
$\Rightarrow$ $P(X < 3)$ = $3 \times \dfrac{1}{{10}} = \dfrac{3}{{10}}$.
Hence, $P(X < 3)$ = $\dfrac{3}{{10}}$.
(iii) $P(X > 6)$.
$\Rightarrow$ $P(X > 6)$ = $P(X = 7)$
$\Rightarrow$ $P(X > 6)$ = $7{k^2} + k = 7 \times {\left( {\dfrac{1}{{10}}} \right)^2} + \dfrac{1}{{10}}$.
$\Rightarrow$ $P(X > 6)$ = $\dfrac{7}{{100}} + \dfrac{1}{{10}} = \dfrac{{7 + 10}}{{100}}$
$\Rightarrow$ $P(X > 6)$ = $\dfrac{{17}}{{100}}$.
Hence, $P(X > 6)$ = $\dfrac{{17}}{{100}}$.
(iv) $P(0 < X < 3)$.
$\Rightarrow$ $P(0 < X < 3)$= $P(X = 1) + P(X = 2)$.
$\Rightarrow$ $P(0 < X < 3)$= $k + 2k = 3k$
$\Rightarrow$ $P(0 < X < 3)$= $3 \times \dfrac{1}{{10}} = \dfrac{3}{{10}}$
Hence , $P(0 < X < 3)$ = $\dfrac{3}{{10}}$.

Note: Whenever we are asked this type of question, first we have to remember the basic points of the probability distribution of a random variable. As according to the questions asked we will use the properties and formulae of probability distribution, we can easily solve them and we will get the required answers.