Question

A ramp is constructed in a parabolic shape such that the height y of any point on its surface is given in terms of the point's horizontal distance x from the bottom of the ramp be $y = \dfrac{{{x^2}}}{{2L}}$​. A block of granite is to be set on the ramp; the coefficient of static friction is 0.80. What is the maximum x coordinate at which the block can be placed on the ramp so that it will remain at rest, if L=10m?

A. 8 m
B. 8.4 m
C. 9 m
D. 9.4 m

Answer 1

The coefficient of static friction is the ratio of friction force over normal force. Frictional force is the vertical force and normal force is the horizontal force. After substituting the force values we will be getting the coefficient friction as the slope. Slope is the ratio of change in y-coordinates over the change in x-coordinates. Use this info to solve the rest of the problem.

Complete step by step answer:
We are given that a ramp is constructed in a parabolic shape such that the height y of any point on its surface is given in terms of the point's horizontal distance x from the bottom of the ramp be $y = \dfrac{{{x^2}}}{{2L}}$​. A block of granite is to be set on the ramp; the coefficient of static friction is 0.80.
We have to find the maximum distance at which the block must be placed so that it will remain at rest.

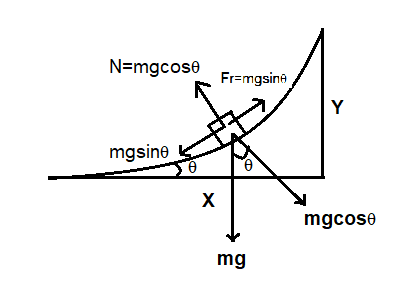
Coefficient of friction is the ratio of frictional force to the normal force.
Frictional force is the vertical force which is $mg\sin \theta$
Normal force is the horizontal force which is $mg\cos \theta$
Therefore,
$COF = \dfrac{{{F_{friction}}}}{{{F_{normal}}}} = \dfrac{{mg\sin \theta }}{{mg\cos \theta }} = \tan \theta$
We know that $\tan \theta$ is the slope, and slope is the ratio of change in y and change in x.
$\tan \theta = \dfrac{{dy}}{{dx}}$ and $y = \dfrac{{{x^2}}}{{2L}}$
Therefore,
$\dfrac{{dy}}{{dx}} = \dfrac{d}{{dx}}\left( {\dfrac{{{x^2}}}{{2L}}} \right) \\\ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{{2x}}{{2L}} = \dfrac{x}{L} \\\$
On equating the value of slope to coefficient of friction, we get
$COF = \tan \theta = \dfrac{{dy}}{{dx}} = \dfrac{x}{L} \\\ \Rightarrow COF = \dfrac{x}{L} \\\$
But we know that the value of coefficient of static friction is 0.8 and the value of L is 10m.
$\Rightarrow COF = \dfrac{x}{L} = 0.8 \\\ \Rightarrow \dfrac{x}{L} = 0.8 \\\ \Rightarrow \dfrac{x}{{10}} = 0.8 \\\ \Rightarrow x = 0.8 \times 10 = 8m \\\$
Therefore, the maximum x-coordinate distance to put the block in rest is 8 m.

The correct option is Option A.

Note: Single force, when it is directed at an angle to the horizontal, is separated into two forces which have different directions and their equivalent results in the main force. This is called resolution of force. Do not confuse horizontal force with vertical force. As the angle with the horizontal increases, the horizontal force decreases, and when the angle with the horizontal decreases, the vertical force increases.