Question

A railway carriage has its center of gravity at a height of 1 m above the rails, which are 1.5 m apart. The maximum safe speed at which it could travel around an unbanked curve of a radius 100 m is

Answer 1

As the railway carriage moves in a curved path, it experiences a centripetal force, which tries to rotate the carriage towards the curve. However, the gravitational force pulls it down by counteracting the torque by the centripetal force, therefore prevents the carriage from being derailed.

Complete step by step answer:
Consider a railway carriage of mass $m$ travelling with a velocity v, on an unbanked circular railway track of radius $r=100\,m$.

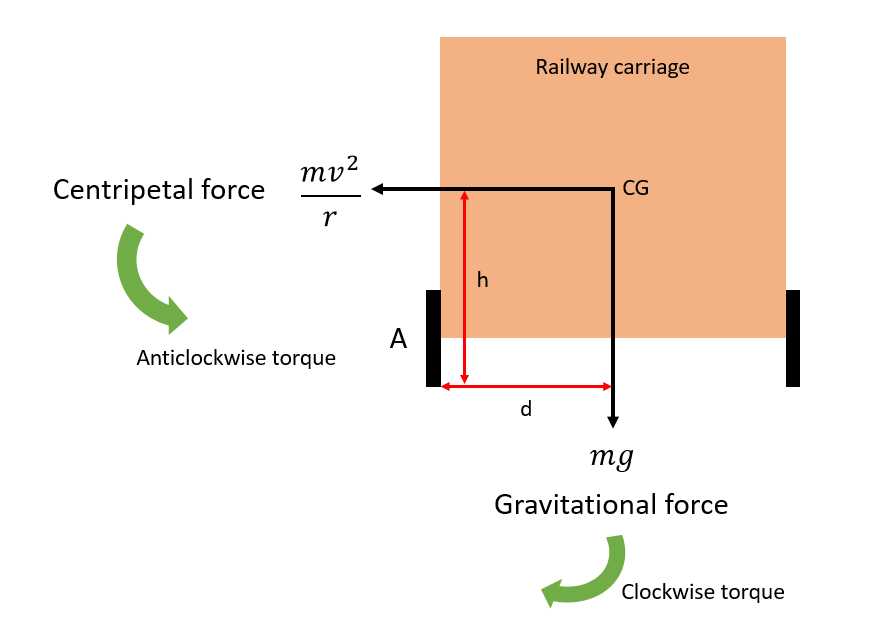
As the carriage travels along the curved railway track, it experiences a centripetal force, acting towards the center of the circular track. This centripetal force acting on the carriage applies an anticlockwise torque about the inner wheel (shown as A) and tries to bend/rotate the carriage in an anticlockwise direction. Simultaneously, the weight of the carriage (or, the gravitational force) applies a clockwise torque about the inner wheel A, bending/rotating the carriage in a clockwise direction, therefore preventing the carriage to get derailed. The whole scenario can be understood from the above diagram.
So let us come to the calculation part now. The centripetal force ${{F}_{C}}$ acting on the carriage is
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$
And the gravitational force (or, the weight of carriage) ${{F}_{G}}$ is
${{F}_{G}}=mg$
As mentioned in the question, the centre of gravity of the carriage is located 1 m above the rails, i.e.$h=1\,m$, and the distance between the rails is 1.5 m, i.e. $2d=1.5\,m$. So to prevent the carriage from the derailment, the maximum velocity of the carriage should be ${{v}_{max}}$, such that about A, the clockwise torque due to the gravitational force counterbalances the anticlockwise torque due to the centripetal force. Therefore,
$\begin{aligned} & \text{Clockwise torque due to gravitational force}=\text{Anticlockwise torque due to centripetal force} \\\ & \text{mg}\times d=\dfrac{mv_{max}^{2}}{r}\times h \\\ & {{v}_{max}}=\sqrt{\dfrac{g\times d\times r}{h}} \\\ & {{v}_{max}}=\sqrt{\dfrac{9.8\times 0.75\times 100}{1.0}} \\\ & {{v}_{max}}\approx 27\,m/s \\\ \end{aligned}$

Hence, the maximum safe speed at which the railway carriage must travel around an unbanked curve without being derailed is 27 m/s.

Note:
- If the speed of the railway carriage is more than the safe speed (in this case 27 m/s), then the anticlockwise torque due to the centripetal force will be greater than the clockwise torque due to gravitational force, therefore rotating the carriage in the anticlockwise direction, leading to an accident.
- This question can be solved quickly by using the formula:
$\tan \theta =\dfrac{v_{max}^{2}}{rg}$
Here, $\tan \theta =\dfrac{h}{d}$. Therefore using the above formula for solving, we get
$\begin{aligned} & \dfrac{h}{d}=\dfrac{v_{max}^{2}}{rg} \\\ & \Rightarrow \dfrac{1}{0.75}=\dfrac{v_{max}^{2}}{100\times 9.8} \\\ & \Rightarrow v_{max}^{2}=\dfrac{100\times 9.8}{0.75} \\\ & \Rightarrow v_{max}^{2}=1306.67 \\\ & \Rightarrow v_{max}^{{}}\approx 27\,m/s \\\ \end{aligned}$