Question
Question: A radioactive nuclide X decays into nuclei Y and Z by simultaneous disintegration as shown. Effectiv...
A radioactive nuclide X decays into nuclei Y and Z by simultaneous disintegration as shown. Effective decay constant for the disintegration is
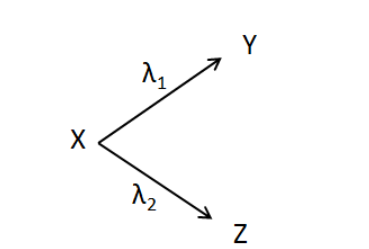
(A) λ1+λ2
(B) λ1+λ2λ1λ2
(C) 2λ1+λ2
(D) λ1+λ22λ1λ2
Solution
To solve this question, we need to use the general equation for the rate of nuclear disintegration. We have to apply the equation separately for the two decays of the given nucleus, and combine them to get the effective decay constant.
Complete step-by-step solution:
We know that the rate of the radioactive decay of a nucleus is proportional to the number of nuclei. And the constant of this proportionality is the decay constant. So the expression for the rate of the radioactive decay of a nucleus is written as
−dtdN=λN
Now, according to the given nuclide X is being decayed into the two daughter nuclei Y and Z. And the decay constants for these two decays are given to be λ1 and λ2 respectively.
So we can separately write the equation for the rate of decay for these two decays. Writing the equation for the decay of X to Y, we get
−dtdNX=λ1NX
Every decayed nucleus of X produces a nucleus Y. So we can write
dtdNY=λ1NX...................(1)
Similarly for the decay of X to Z, we can write
dtdNZ=λ2NX.....................(2)
Adding (1) and (2) we have
dtdNY+dtdNZ=λ1NX+λ2NX
⇒dtd(NY+NZ)=(λ1+λ2)NX (3)
Now, since Y and Z nuclei are produced from the nucleus X, so we can write
dtd(NY+NZ)=−dtdNX
Substituting this above, we get
−dtdNX=(λ1+λ2)NX
Comparing with the general decay rate equation −dtdN=λN, we get the effective decay constant for the given disintegration as
λ=λ1+λ2
Thus, the effective decay constant for the disintegration of the nucleus X into the nuclei Y and Z is equal to λ1+λ2.
Hence, the correct answer is option A.
Note: The phenomenon of radioactivity is used on a large scale to generate electric power. Also, it is used in the diagnosis and treatment of diseases in the field of nuclear medicine. The diseases which can be treated by radioactivity are thyroid, cancers etc.
