Question

A radioactive nucleus initially at rest decays by emitting an electron and neutrino at right angles to one another.
The momentum of the electron is $3.2\times {{10}^{-23}}kgm{{s}^{-1}}$ and that of the neutrino is $6.4\times {{10}^{-23}}kgm{{s}^{-1}}$. The direction of the recoiling nucleus with that of the electron motion is:
A.) ${{\tan }^{-1}}(0.5)$
B.) ${{\tan }^{-1}}(2)$
C.) $\pi -{{\tan }^{-1}}(2)$
D.) $\dfrac{\pi }{2}+{{\tan }^{-1}}(2)$

Answer 1

Hint: Here, we are not applying any external force. The nucleus will undergo decay. During the decay of the nucleus, electrons and neutrons are emitting in a particular direction. Their momentum will combine and the resultant momentum will go through a specific direction. The nucleus momentum will be in the opposite direction to this resultant momentum of the neutron and electron due to the conservation of linear momentum. By computing the angles between them, we can find out the angle between the momentum direction of the electron and the momentum direction of the nucleus.

Complete step by step answer:
According to the question, the electron and neutron from a radioactive nucleus are taking perpendicular paths after the decay. Both particles momentum is given in the question. Decay will produce a recoil to the nucleus. The recoil of the nucleus is exactly due to the conservation of momentum. The graphical representation of the radioactive nucleus decay is shown below.

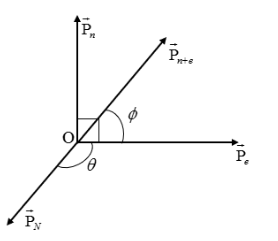
According to the diagram, the nucleus is placed at the origin O. After the decay, the direction of the momentum of neutron $(\overset{\to }{\mathop{{{P}_{n}}}}\,)$ and direction of the momentum of the electron $(\overset{\to }{\mathop{{{P}_{e}}}}\,)$ is perpendicular to each other. The combined momentum of neutron and electron $\text{(}\overset{\to }{\mathop{{{P}_{n+e}}}}\,)$ will balance the recoil momentum of the nucleus $(\overset{\to }{\mathop{{{P}_{N}}}}\,)$ due to the conservation of momentum. Here the direction of the momentum of the electron and the direction of the combined electron and neutron will make an angle $\phi \text{ }$. This can find out from the direction of the momentum of the electron and momentum of the neutron.

According to the diagram,

$\tan \phi =\dfrac{\overset{\to }{\mathop{{{P}_{n}}}}\,}{\overset{\to }{\mathop{{{P}_{e}}}}\,}\text{ }$

We have already given the momentum of electrons and neutrons.

$\overset{\to }{\mathop{{{P}_{n}}}}\,=6.4\times {{10}^{-23}}kgm{{s}^{-1}}$
$\overset{\to }{\mathop{{{P}_{e}}}}\,=3.2\times {{10}^{-23}}kgm{{s}^{-1}}$
Now we can find the $\tan \phi$.
$\dfrac{\overset{\to }{\mathop{{{P}_{n}}}}\,}{\overset{\to }{\mathop{{{P}_{e}}}}\,}=\dfrac{6.4\times {{10}^{-23}}kgm{{s}^{-1}}}{3.2\times {{10}^{-23}}kgm{{s}^{-1}}}$
$\tan \phi =2$

According to the law of conservation of momentum, the combined momentum will be equal to the momentum of the nucleus. The direction will be opposite to the direction of combined particles momentum. Here, the momentum of the nucleus and momentum of an electron makes an angle $\theta$.

From the diagram,

$\theta =\pi -\phi$
As we know, $\phi ={{\tan }^{-1}}(2)$

Therefore,

$\theta =\pi -{{\tan }^{-1}}(2)$

So, the correct answer is option C.

Note: It is better to use a diagram to understand the travel and direction of particles. Without finding the angle between the resultant momentum of electron and neutron and the momentum of the electron, we can’t find the angle between the recoiling nucleus and electron motion. Here conservation of momentum is used to support the law of action and reaction. If we are applying any external forces to the system, we have to consider that also to calculate the problem.