Question
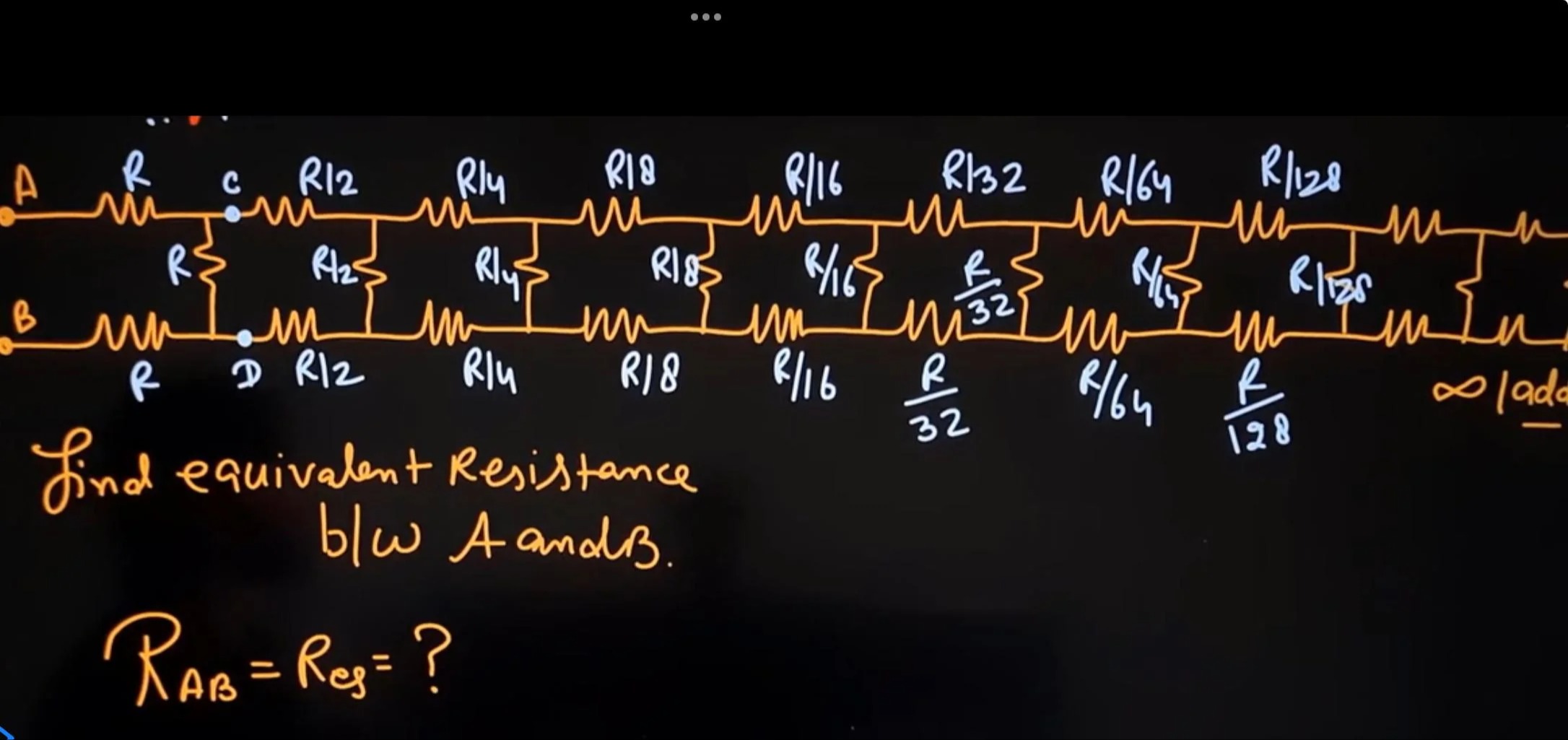
Question: Find equivalent Resistance blw A and B. $R_{AB}$=$R_{eq}$ = ? A R c R/2 R/4 R/8 R/16 R/32 R/64 R/1...
Find equivalent Resistance blw A and B.
RAB=Req = ?
A R c R/2 R/4 R/8 R/16 R/32 R/64 R/128
B R D R/2 R/4 R/8 R/16 32R R/64 128R ∞/ladder
R(21+17)
Solution
The problem describes an infinite ladder network where the resistances in each subsequent section are scaled by a factor of 1/2. Let the equivalent resistance between points A and B be Req.
The first "unit" of the ladder consists of:
- A resistor of value R in the upper branch (between A and C). Let's call this RAC.
- A resistor of value R in the lower branch (between B and D). Let's call this RBD.
- A vertical resistor of value R connecting the upper and lower branches (between C and D). Let's call this RCD1.
The network to the right of points C and D is an infinite ladder. All the resistances in this part of the network are half of the corresponding resistances in the original ladder. For example, the next horizontal resistors are R/2, the next vertical resistor is R/2, and so on. Therefore, if the equivalent resistance of the entire ladder from A to B is Req, then the equivalent resistance of the infinite ladder starting from C and D will be Req/2. Let's call this RCD_ladder.
Now, we can redraw the circuit by replacing the infinite ladder to the right of C and D with its equivalent resistance RCD_ladder=Req/2.
The circuit between points C and D now has two resistors in parallel:
- The vertical resistor RCD1=R.
- The equivalent resistance of the rest of the ladder RCD_ladder=Req/2.
The equivalent resistance between C and D, due to these parallel components, is: RCD_parallel=RCD1∥RCD_ladder RCD_parallel=R+(Req/2)R×(Req/2) RCD_parallel=2R+ReqR⋅Req
Now, the entire circuit from A to B can be viewed as three resistors in series:
- RAC (from A to C)
- RCD_parallel (from C to D)
- RBD (from D to B)
So, the equivalent resistance Req is: Req=RAC+RCD_parallel+RBD Substitute the values: RAC=R, RBD=R. Req=R+2R+ReqR⋅Req+R Req=2R+2R+ReqR⋅Req
Now, we solve this equation for Req. Let X=Req. X=2R+2R+XRX Multiply both sides by (2R+X): X(2R+X)=2R(2R+X)+RX 2RX+X2=4R2+2RX+RX 2RX+X2=4R2+3RX Rearrange the terms to form a quadratic equation: X2−RX−4R2=0
Using the quadratic formula X=2a−b±b2−4ac, where a=1, b=−R, c=−4R2: X=2(1)−(−R)±(−R)2−4(1)(−4R2) X=2R±R2+16R2 X=2R±17R2 X=2R±R17 Since resistance must be a positive value, we take the positive root: Req=2R+R17 Req=R(21+17)
The final answer is R(21+17).
Explanation of the solution:
- Identify the repeating pattern: The network is an infinite ladder where each subsequent section's resistances are scaled by 1/2.
- Define equivalent resistance: Let the equivalent resistance of the entire infinite ladder be Req.
- Utilize infinite ladder property: Due to the scaling, the equivalent resistance of the ladder starting from the second set of nodes (C and D) is Req/2.
- Simplify the first section: The vertical resistor (R) in the first section is in parallel with the equivalent resistance of the rest of the ladder (Req/2). Calculate this parallel combination.
- Formulate the equation: The two horizontal resistors (R each) in the first section are in series with the calculated parallel combination. Set up an equation for Req.
- Solve the quadratic equation: Solve the resulting quadratic equation for Req, choosing the positive root as resistance cannot be negative.
