Question
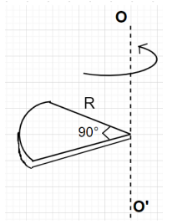
Question: A quarter disc of radius R and mass m is rotating about the axis OO’ (perpendicular to the plane of ...
A quarter disc of radius R and mass m is rotating about the axis OO’ (perpendicular to the plane of the disc) as shown. What is the rotational kinetic energy of the quarter disc?
Solution
Hint- Here, we will proceed by finding the moment of inertia of a quarter disc of mass m and radius R using the formula for the moment of inertia of complete circular disc and then we will use the formula for rotational kinetic energy.
Formulas Used- KE = 21Iω2
Step By Step Answer:
The rotational kinetic energy can be expressed in the form as given under for a given fixed axis of rotational.
Rotational kinetic energy, KE = 21Iω2 →(1) where I represents the moment of inertia of the body about the fixed axis and ω represents the angular velocity of the body
As we know that the moment of inertia of a complete circular disc of mass M and radius R about its vertical axis passing through its centre is given by
Idisc=2MR2
Since, if this complete circular disc is divided into four equal quarter disks (each of mass m and radius R) then the moment of inertia due to each of these quarter disk is equal and the sum of all these moments of inertia of four quarter disks will be equal to that of the complete circular disk about the vertical axis passing through the centre.
i.e., 4(Moment of a quarter disk having mass r and radius R about the vertical axis passing through its centre) = Moment of inertia of the complete circular disc having mass M and radius R about the vertical axis passing through its centre
⇒ 4(Moment of a quarter disk having mass r and radius R about the vertical axis passing through its centre) = Idisc=2MR2
⇒ Moment of a quarter disk having mass r and radius R about the vertical axis passing through its centre = 4Idisc=2×4MR2=8MR2
By substituting M = 4m in the above expression, we get
⇒ Moment of a quarter disk having mass r and radius R about the vertical axis passing through its centre = 84mR2=2mR2
Using the above formula, we can write
Moment of the given quarter disk having mass r and radius R about the axis OO’ I=2mR2
Using the formula given in equation (1), we get
Rotational kinetic energy of the quarter disc = 21(2mR2)ω2=41mR2ω2
Therefore, option B is correct.
Additional Information:
A rotating object's kinetic energy is analogous to linear kinetic energy, and can be expressed in terms of moment of inertia and angular velocity. The total kinetic energy of an object can be written as the sum of the translational kinetic energy of the center of mass and the rotational kinetic energy about the centre of mass.
Note- In this particular problem, we have written M = 4m because four similar quarter disc each having mass m and radius R is making up the complete disc of mass M and radius R. Also, here the axis of rotation OO’ is fixed and the disc is not doing any translational motion it is just doing rotational motion.
