Question

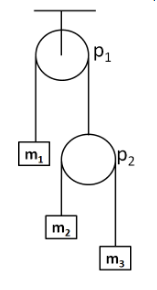
A pulley-rope-mass arrangement is shown in figure. Find the acceleration of block ${m_1}$ when the masses are set free to move. Assume that the pulleys and the ropes are ideal.

Answer 1

To solve this question, we need to apply the Newton’s second law of motion to each of the three blocks after considering their free body diagrams. On solving the equations formed, we can get the required acceleration of ${m_1}$ .

Complete Answer:
Let the tension in the string connecting the blocks of masses ${m_2}$ and ${m_3}$ be $T$ . Also, the tension in the string connecting the block of mass ${m_1}$ with the pulley ${P_2}$ be ${T_1}$ . So the free body diagram of the pulley ${P_2}$ is as shown in the below diagram.

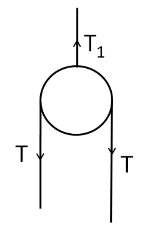
Since the pulley is massless, so from the Newton’s second law of motion, the net force on the pulley ${P_2}$ must be equal to zero. So we have
${T_1} - T - T = 0$
$\Rightarrow {T_1} = 2T$ ..............................(1)
Let the acceleration of the block of masses ${m_1}$ , ${m_2}$ and ${m_3}$ be ${a_1}$ , ${a_2}$ and ${a_3}$ respectively.
Since the pulley ${P_2}$ is connected with the block of mass ${m_1}$ , so its acceleration is also equal to ${a_1}$ .
Now, considering the free body diagram of the block of mass ${m_1}$ , we have the following figure

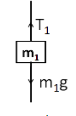
From the Newton’s second law of motion, we can write
${T_1} - {m_1}g = {m_1}{a_1}$
From (1) we can write
$2T - {m_1}g = {m_1}{a_1}$ ..............................(2)
Now, the masses ${m_2}$ and ${m_3}$ are connected to the pulley ${P_2}$ which is itself accelerating with acceleration ${a_1}$ , so we consider their motion with respect to the pulley to get the equation
${a_2} - {a_1} = - \left( {{a_3} - {a_1}} \right)$
$\Rightarrow 2{a_1} = {a_2} + {a_3}$ ..............................(3)
So considering the free body diagrams of ${m_2}$ and ${m_3}$ , we can write the following equations
${m_2}g - T = {m_2}{a_2}$ ..............................(4)
$T - {m_3}g = {m_3}{a_3}$ ..............................(5)
Multiplying both sides of (4) by ${m_3}$ we get
${m_2}{m_3}g - {m_3}T = {m_2}{m_3}{a_2}$ ..............................(6)
Multiplying both sides of (5) by ${m_2}$ we get
${m_2}T - {m_2}{m_3}g = {m_2}{m_3}{a_3}$ ..............................(7)
Adding (6) and (7) we have
$\left( {{m_2} - {m_3}} \right)T = {m_2}{m_3}\left( {{a_2} + {a_3}} \right)$
Putting (3) in the above equation, we get
$\left( {{m_2} - {m_3}} \right)T = 2{m_2}{m_3}{a_1}$
$\Rightarrow T = \dfrac{{2{m_2}{m_3}}}{{\left( {{m_2} - {m_3}} \right)}}{a_1}$
Putting this in (2) we have
$\dfrac{{4{m_2}{m_3}}}{{\left( {{m_2} - {m_3}} \right)}}{a_1} - {m_1}g = {m_1}{a_1}$
$\Rightarrow \left( {\dfrac{{4{m_2}{m_3}}}{{\left( {{m_2} - {m_3}} \right)}} - {m_1}} \right){a_1} = {m_1}g$
On simplifying we get
$\left( {\dfrac{{4{m_2}{m_3} - {m_1}\left( {{m_2} - {m_3}} \right)}}{{\left( {{m_2} - {m_3}} \right)}}} \right){a_1} = {m_1}g$
$\Rightarrow {a_1} = \dfrac{{{m_1}\left( {{m_2} - {m_3}} \right)g}}{{4{m_2}{m_3} - {m_1}\left( {{m_2} - {m_3}} \right)}}$
Hence, this is the required acceleration of the block of mass ${m_1}$ .

Note:
Do not combine the blocks ${m_2}$ and ${m_3}$ as a single block to write the acceleration of the block ${m_1}$ . This is because the motion of these blocks will affect the acceleration of ${m_1}$ .