Question

A pulley of radius 2m is rotated about its axis by a force $F=(20t-5{{t}^{2}})N$ (Where, t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is $10kg{{m}^{2}}$, then the number of rotations made by the pulley before its direction of motion is reserved, is:
(A). More than 3 but less than 6
(B). More than 6 but less than 9
(C). More than 9
(D). Less than 3

Answer 1

Hint: Here we are applying force to rotate a pulley. Before stopping it will do some rotations. Since we have already given the force that we are applying, the moment of inertia of the pulley and the radius of the pulley, we can apply the same laws of linear motion to the rotational motion.

Formula used:
$\tau =I\alpha$, where $I$ is the moment of inertia and $\alpha$ is the angular acceleration.
$\tau =Fr$, here force is applied tangentially to the pulley. So the force direction and direction of the radius will be perpendicular.
$\alpha =\dfrac{d\omega }{dt}$, where $\omega$ is the angular velocity.

Complete step by step answer:

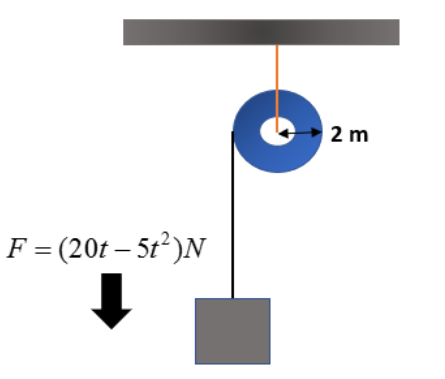
Consider a pulley of radius 2 m. Its moment of inertia about the axis is already given in the question. It is about $10kg{{m}^{2}}$. We are applying an external force tangentially to the pulley. Here we are considering the rotational motion. According to the laws of rotational motion, torque can be written as,
$\tau =I\alpha$, where $I$ is the moment of inertia and $\alpha$ is the angular acceleration. Here we are going to find out the number of rotations before the direction of motion is reserved. So the work done will be zero.
$\int{\tau d\theta =0}$, where $\theta$ is the angular displacement.
Torque can find out from the force and radius of the pulley.
$\tau =Fr$, here force is applied tangentially to the pulley. So the force direction and direction of the radius will be perpendicular.
$\tau =(20t-5{{t}^{2}})\times 2$
$\tau =40t-10{{t}^{2}}$
Next, we can find out the angular acceleration from the torque.
$\alpha =\dfrac{40t-10{{t}^{2}}}{I}$
$\alpha =\dfrac{40t-10{{t}^{2}}}{10}$
$\alpha =4t-{{t}^{2}}$
As we know angular acceleration is the derivative of angular velocity. Thus, we can write as,
$\alpha =\dfrac{d\omega }{dt}$, where $\omega$ is the angular velocity.
$d\omega =\alpha dt$
So that we have to integrate this, to find out the angular velocity.
$\int{d\omega }=\int{\alpha dt}$
Here we are going to integrate from 0 to t.
$\int\limits_{0}^{t}{d\omega }=\int\limits_{0}^{t}{(4t-{{t}^{2}}})dt$
$\omega =\left[ 2{{t}^{2}}-\dfrac{{{t}^{3}}}{3} \right]_{0}^{t}$
Now we can assign the limits to the equation.
$\omega =\left[ 2{{t}^{2}}-\dfrac{{{t}^{3}}}{3} \right]$
Angular velocity will be zero at a point. So we can find out the time at which the velocity will be zero.
$2{{t}^{2}}-\dfrac{{{t}^{3}}}{3}=0$
$2{{t}^{2}}=\dfrac{{{t}^{3}}}{3}$
$t=6s$
The angular velocity will be zero within 6 seconds.
Now we can find out the angular displacement from 0 to 6 seconds.
$\theta =\int\limits_{0}^{6}{\omega dt}$
We can assign the angular velocity equation here.
$\theta =\int\limits_{0}^{6}{\left[ 2{{t}^{2}}-\dfrac{{{t}^{3}}}{3} \right]dt}$
$\theta =\left[ \dfrac{2{{t}^{3}}}{3}-\dfrac{{{t}^{4}}}{12} \right]_{0}^{6}$
We can put the limits to the equation.
$\theta =\left[ \dfrac{216}{3}-\dfrac{1296}{12} \right]$
$\theta =\left[ 144-108 \right]=36rad$
So, the number of revolutions will be $\dfrac{36}{2\pi }$, since 36 is the total angular displacement.
Therefore the revolutions will be less than 6. So the correct option is A.

Note: Do not forget to make the angular velocity as zero. Then only we can find out the time period required for the stopping of the pulley. During this time it will move 36-radians angular displacement. So do not stop the calculation there. Because we have calculated the total angular displacement. We have to calculate the number of rotations from there. It may not be an integer value. That’s why the options are given in a range.