Question

A proton takes ${{10}^{-12}}$ seconds to complete one revolution in a uniform magnetic field. The time taken in another orbit of double the radius in the same field is
$\begin{aligned} & a)0.5\times {{10}^{-12}}seconds \\\ & b)2\times {{10}^{-12}}seconds \\\ & c)4\times {{10}^{-12}}seconds \\\ & d){{10}^{-12}}seconds \\\ \end{aligned}$

Answer 1

The charged particle enters the magnetic field with some initial velocity v. Since the direction of motion is perpendicular to the magnetic field the charge will move in a circular path due to the force because of the magnetic field. Hence we can equate the force due to the magnetic field as the centripetal force acting on the charge while moving in a circular path. Therefore the radius of the circular path can be calculated from the required expression obtained. The time period of revolution of the charged particle moving in a circle of radius r and velocity v is given as the ratio of circumference of the circle to the speed of the charged particle. Hence we can determine the time period for the charge particle to revolve in a circle of double radius.

Formula used: ${{F}_{B}}=q\left( v\times B \right)$
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}$
$t=\dfrac{2\pi r}{v}\sec$

Complete step by step answer:

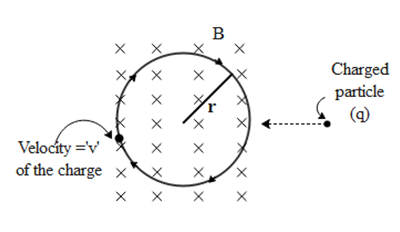
The force due to magnetic field on the charge is given by ${{F}_{B}}=q\left( v\times B \right)...(1)$, (where q is the charge of the particle v it its velocity while entering the magnetic field and B is the magnitude of the field). As the charged particle moves in the circle we can also write the centripetal force on the charge i.e.
${{F}_{C}}=\dfrac{m{{v}^{2}}}{r}...(2)$ where m is the mass of the particle, v is the velocity and r is the radius of the circular orbit.
The time period of revolution of the charged particle moving in a circle of radius r and velocity v is given as,$t=\dfrac{2\pi r}{v}\sec ...(3)$.
In the magnetic field the particle moves in a circular path, hence we can write the magnetic force equals the centripetal force. Therefore using equation 1 and 2 we get,
$\begin{aligned} & {{F}_{B}}={{F}_{C}} \\\ & q\left( v\times B \right)=\dfrac{m{{v}^{2}}}{r} \\\ & qv.B\operatorname{Sin}\theta =\dfrac{m{{v}^{2}}}{r},\text{since }\\!\\!\theta\\!\\!\text{ =9}{{\text{0}}^{\text{o}}}\text{ Sin9}{{\text{0}}^{\text{o}}}\text{=1, i}\text{.e}\text{. the particle enters perpendicular to the field} \\\ & qB=\dfrac{mv}{r} \\\ & r=\dfrac{mv}{qB} \\\ \end{aligned}$
If we see the above equation if we increase the radius of the circular path the velocity of the charge will also increase twice as all the other quantities remain constant.
It is given in the question that the time that the time period of revolution for the radius r is ${{10}^{-12}}$. There substituting this equation 3 we get,
$\begin{aligned} & t=\dfrac{2\pi r}{v}\sec \\\ & {{10}^{-12}}=\dfrac{2\pi r}{v} \\\ \end{aligned}$
As the radius is increased twice the velocity will also increase by the same, hence
$\begin{aligned} & {{10}^{-12}}=\dfrac{2\pi \left( 2r \right)}{2v} \\\ & {{10}^{-12}}=\dfrac{2\pi \left( r \right)}{v} \\\ \end{aligned}$
Hence we can conclude that the time period of revolution of the proton when the radius of the is doubled remains the same.

So, the correct answer is “Option D”.

Note: The particle actually starts going in a circular path as the cross product taken between v and B is the curl of two vectors. The charge initially possesses some kinetic energy while entering the magnetic field B. Hence the radius of the path covered by the charge is directly proportional to the square root of the kinetic energy of the charge particle.