Question
Question: A proton of mass m collides elastically with a particle of unknown mass at rest. After the collision...
A proton of mass m collides elastically with a particle of unknown mass at rest. After the collision, the proton and the unknown particle are seen moving at an angle of 900 with respect to each other. The mass of unknown particle is:
A.3m
B. 2m
C.2m
D.m
Solution
Hint: Since it is an elastic collision, the conservation of momentum and conservation of kinetic energy will be needed. We also need to remember which are vector quantities and which are scalar quantities.
Step by step solution:
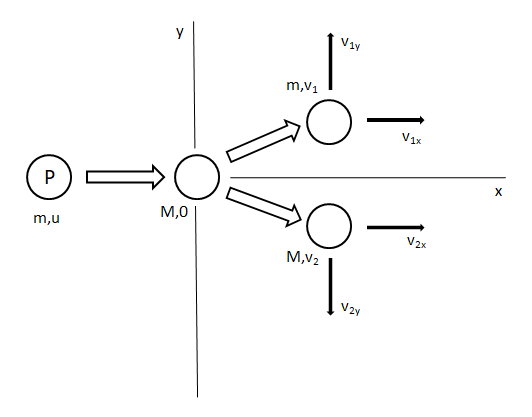
We know the proton’s mass is m having initial velocity u. Let’s consider the unknown mass as M and since it is at rest, its velocity is zero. After the collision the proton moves with velocityv1, making an angle θ1 with the horizontal. Similarly, M moves with velocity v2 making an angle θ2 with the horizontal.
After collision, the velocity component of mass m will be divided into 2 components along the x and y axes, since it’s a vector quantity. We will call them v1x and v1y respectively.
v1x=v1cosθ1 and v1y=v1sinθ1.
Similarly, the velocity components of v2 will be divided into v2x and v2y, for velocity components along x and y axes respectively.
v2x=v2cosθ2 and v2y=−v2sinθ2.
Let’s consider, both the masses are equal and try and see if we are getting the condition of θ1+θ2=900.
pxinitial = px final using conservation of momentum along the x axis.
mu=mv1cosθ1+mv2cosθ2
u=v1cosθ1+v2cosθ2→(1)
pyinitial = py final using conservation of momentum along the x axis.
0+0=v1sinθ1−v2sinθ2
0=v1sinθ1−v2sinθ2→(2)
(1)2+(2)2 gives us,
u2=(v1cosθ1+v2cosθ2)2+(v1sinθ1−v2sinθ2)2
u2=v12cos2θ1+v22cos2θ2+2v1v2cosθ1cosθ2+v12sin2θ1+v22sin2θ2−2v1v2sinθ1sinθ2
u2=v12(cos2θ1+sin2θ1)+v22(cos2θ2sin2θ2)+2v1v2(cosθ1cosθ2−sinθ1sinθ2)
u2=v12+v22+2v1v2cos(θ1+θ2)→(3)
Now, using the conservation of kinetic energy formula:
21mu2=21mv12+21mv22
Here, we don’t use the velocity components along each axis as Energy is a scalar quantity and direction component isn’t required.
u2=v12+22→(4)
Comparing the equations (3) and (4), we get:
2v1v2cos(θ1+θ2)=0
cos(θ1+θ2)=0
As we know that cos(2nπ)=0 for n= any integer except zero.
Considering the case for n=1, we get, θ1+θ2=2π
This is the same condition as given in the question; hence our consideration of both the masses having the same mass is correct. Hence, unknown mass is m.
Note:
Here we need to remember to break the velocity to its components.
The velocity component along the axis needs to be considered as per the axis, hence the y component of velocity for unknown mass is negative.
