Question

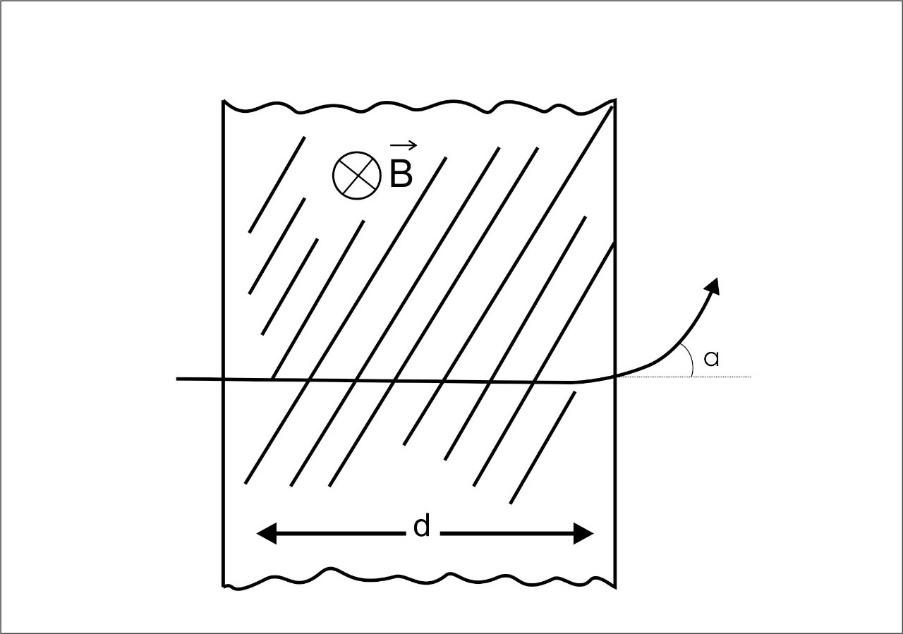
A proton (mass m) accelerated by a potential difference V files through a uniform transverse magnetic field B. The field occupies a region of space by width ‘d’. If $\alpha$ be the angle of deviations of proton from initial direction of motion (see fig), the value of $\sin \alpha$ will be:

A) $Bd\sqrt {\dfrac{q}{{2mV}}}$
B) $\dfrac{B}{d}\sqrt {\dfrac{{qd}}{{mV}}}$
C) $qV\sqrt {\dfrac{{Bd}}{{2m}}}$
D) $\dfrac{B}{d}\sqrt {\dfrac{q}{{2mV}}}$

Answer 1

In this question, first we have to calculate energy of proton $E$ in the term of $v$ , and then have to find the magnetic force $F$. From the given figure we can easily find that $\sin \alpha = \dfrac{d}{R}$ . After putting the value of $R$ we can easily find the value of $\sin \alpha$.

Complete step by step answer:
In this question, A proton (mass m) is accelerated by a potential difference V files through a uniform transverse magnetic field B, and the field occupies a region of space by width ‘$d$ ’. Here, $\alpha$ be the angle of deviation of proton from initial direction of motion .we need to calculate, the value of $\sin \alpha$.
Given that,
$m =$ Mass of proton
$V =$ Potential difference
$v =$ Velocity of proton
$e =$ Charge on proton
$d =$ The field occupies a region of space of width.
$R =$ The radius of circle
$\alpha =$ Angle of deviation
Now, first we have to find the energy of proton,
We know that,
$E = \dfrac{1}{2}m{v^2} = eV$
Hence,
$\Rightarrow v = \sqrt {\dfrac{{2eV}}{m}}$
Now find the magnetic force, we know that magnetic force can be written as,
$\Rightarrow F = e\left( {\overrightarrow v \times \overrightarrow B } \right)$
\Rightarrow \dfrac{{m{v^2}}}{R} \\\ \Rightarrow R = \dfrac{{mv}}{{eB}} \\\
We know that,
$\Rightarrow \sin \alpha = \dfrac{d}{R}$
On putting the value of$R$, we get
$\Rightarrow \sin \alpha = \dfrac{{deB}}{{mv}} \\\ \Rightarrow \sin \alpha = \dfrac{{deB}}{m}\sqrt {\dfrac{m}{{2eV}}} \\\ \Rightarrow \sin \alpha = Bd\sqrt {\dfrac{e}{{2mV}}} \\\$
$e$ can be written as $q$, which is the symbol of charge, thus the equation become, $\sin \alpha = Bd\sqrt {\dfrac{q}{{2mV}}}$

Therefore, the correct option is A.

Note: As we know that the force is the vector quantity and the cross product of the velocity and the magnetic field provide the vector quantity. And we know the correct value of $R$ is obtained as $\sin \alpha = \dfrac{d}{R}$.