Question

A proton accelerated by a potential difference of 500 kV moves through a transverse magnetic field of $0.51{\text{ }}T$ as shown in the figure. Then the angle $\theta$ through which the proton deviates from the initial direction of its motion is(approximately)

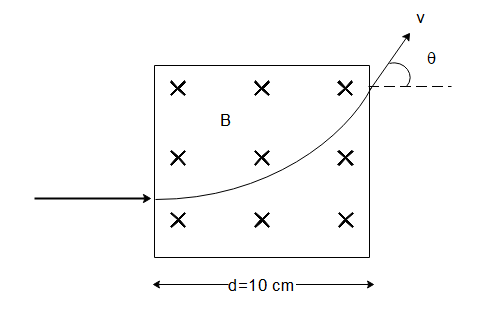
(A) $15^\circ$
(B) $30^\circ$
(C) $45^\circ$
(D) $60^\circ$

Answer 1

When the charged particle enters the charged region of the magnetic field, it will be deflected by the magnetic field and try to execute a circular motion. The radius of the circular motion depends on the velocity of the charged particle.

Formula used: In this solution, we will use the following formula:
-Radius of the circular motion of a charged particle in a magnetic field $r = \dfrac{{mv}}{{qB}}$ where $m$ is the mass of the charged particle, $v$ is its velocity, $q$ is the charge, and $B$ is the strength of the magnetic field.

Complete step by step answer:
When a charged particle moves in a magnetic field, it is deflected by the magnetic field. The particle is deflected such that the force of deflection will act perpendicular to its direction of velocity. The direction of the force can be determined by the left-hand rule. The charged particle will execute a circular motion, whose radius will be determined by
$r = \dfrac{{mv}}{{qB}}$
To calculate the radius of the particle, we need the velocity of the object.
We know that the charged particle, a proton accelerated by a potential difference of 500 kV. Hence the change in potential energy of the particle will be converted to kinetic energy as
$q\Delta V = \dfrac{1}{2}m{v^2}$
Substituting the value of $q = 1.6 \times {10^{19}}$, $\Delta V = 5 \times {10^5}\,V$, $m = 9.1 \times {10^{ - 31}}\,kg$ and $B = 0.51T$, we can get the velocity as
$v = 9.78 \times {10^6}\,m/s$
Then the radius of the particle will be determined from $r = \dfrac{{mv}}{{qB}}$ . Looking at the geometry of the charged particle as shown below,

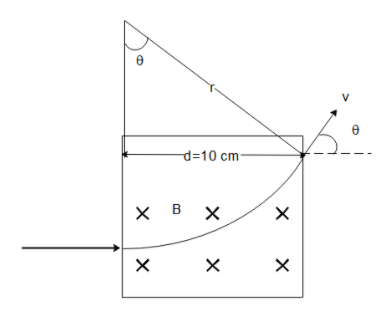
we can write $d = r\sin \theta$
Hence substituting the value of $r = \dfrac{{mv}}{{qB}}$, we get
$\sin \theta = \dfrac{{dqB}}{{mv}}$ which can be calculated as
$\sin \theta = 0.5$
Hence the angle formed by the charged particle will be

$\theta = 30^\circ$ which is an option (B).

Note: The force on the charged particle will be upwards as determined by the movement of the charged particle in a magnetic field facing inside the page. Hence the centre of the circular path will be in the vertically upward direction with the centre of the circle lying on the line containing the beginning of the magnetic field region.