Question

A projectile shot at an angle of $45^\circ$ above the horizontal strikes a building $30\,{\text{m}}$ away at a point $15\,{\text{m}}$ above the point of projection. Find: (a) the speed of projection. (b) the magnitude and direction of velocity of the projectile when it strikes the building.

Answer 1

Use the equation of trajectory of the projectile to calculate the speed of projection of the projectile. Use a kinematic equation and the expression for the horizontal component of the projectile to determine the vertical and horizontal component of the final velocity of the projectile.

Formula used:
The equation for the trajectory of the projectile is given b
$y = x\tan {\theta _0} - \dfrac{1}{2}\dfrac{g}{{{u^2}{{\cos }^2}{\theta _0}}}{x^2}$ …… (1)
Here, $x$ and $y$ are the horizontal and vertical coordinates of the trajectory of the projectile, $u$ is the velocity of projection, ${\theta _0}$ is the angle of projection and $g$ is the acceleration due to gravity.
The kinematic equation relating initial velocity $u$, final velocity $v$, acceleration $a$ and displacement $h$ of an object in the free fall is
${v^2} = {u^2} - 2gh$ …… (2)
The horizontal component of the final velocity ${v_x}$ of the projectile is
${v_x} = u\cos {\theta _0}$
Here, ${\theta _0}$ is the angle of project is the angle of projection of the projectile.

Complete step by step answer
The angle of projection of the projectile is $45^\circ$. The distance of the building from the point of projection is $30\,{\text{m}}$ and the height at which the projectile strikes the building is $15\,{\text{m}}$.
The diagram for the projectile motion of the projectile is as follows:

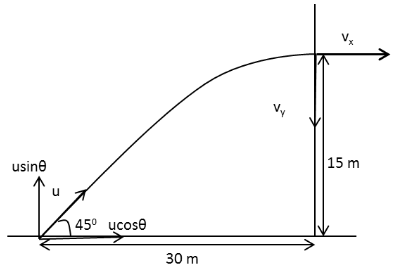
In the above diagram, $u$ is the velocity of projection of the projectile, $u\cos \theta$ and $u\sin \theta$ are the horizontal and vertical components of the velocity of projection and ${v_x}$ and ${v_y}$ are the horizontal and vertical components of the final velocity of the projectile when it strikes the building respectively.
(a) Calculate the speed of projection of the projectile.
The final X and Y coordinates of the trajectory of the projectile when it strikes the building are $30\,{\text{m}}$ and $15\,{\text{m}}$ respectively.
Substitute $15\,{\text{m}}$ for $y$, $30\,{\text{m}}$ for $x$, $45^\circ$ for ${\theta _0}$ and $9.8\,{\text{m/}}{{\text{s}}^2}$ for $g$ in equation (1).
$15\,{\text{m}} = \left( {30\,{\text{m}}} \right)\tan \left( {45^\circ } \right) - \dfrac{1}{2}\dfrac{{9.8\,{\text{m/}}{{\text{s}}^2}}}{{{u^2}{{\cos }^2}45^\circ }}{\left( {30\,{\text{m}}} \right)^2}$
$\Rightarrow u = 14\sqrt 3 \,{\text{m/s}}$
Hence, the speed of projection is $14\sqrt 3 \,{\text{m/s}}$.
(b) Calculate the horizontal and vertical component of the velocity of the projectile when it strikes the building.
The horizontal component of velocity of projectile when it strikes the building is
${v_x} = u\cos {\theta _0}$
Substitute $14\sqrt 3 \,{\text{m/s}}$ for $u$ and $45^\circ$ for $\theta$ in the above equation.
${v_x} = \left( {14\sqrt 3 \,{\text{m/s}}} \right)\left( {{\text{cos}}45^\circ } \right)$
$\Rightarrow {v_x} = 17.15\,{\text{m/s}}$
The horizontal component of the velocity of the projectile when it strikes the building is $17.15\,{\text{m/s}}$.
Rewrite equation (2) for the vertical component of velocity ${v_y}$ of the projectile when it strikes the building.
$v_y^2 = u_y^2 - 2gh$
Here, ${u_y}$ is the vertical component of the velocity of projection and $h$ is the vertical displacement of the projectile when it strikes the building.
Substitute $u\sin {\theta _0}$ for ${u_y}$ in the above equation.
$v_y^2 = {\left( {u\sin {\theta _0}} \right)^2} - 2gh$
Take square root on both sides of the above equation.
${v_y} = \sqrt {{{\left( {u\sin {\theta _0}} \right)}^2} - 2gh}$
Substitute $14\sqrt 3 \,{\text{m/s}}$ for $u$, $45^\circ$ for ${\theta _0}$, $9.8\,{\text{m/}}{{\text{s}}^2}$ for $g$ and $15\,{\text{m}}$ for $h$ in the above equation.
${v_y} = \sqrt {{{\left( {\left( {14\sqrt 3 \,{\text{m/s}}} \right)\left( {{\text{sin}}45^\circ } \right)} \right)}^2} - 2\left( {9.8\,{\text{m/}}{{\text{s}}^2}} \right)\left( {15\,{\text{m}}} \right)}$
$\Rightarrow {v_y} = 0\,{\text{m/s}}$
The vertical component of the velocity of the projectile when it strikes the building is zero.
Since the vertical component of the final velocity of the projectile is zero, the projectile has velocity in the horizontal direction when it strikes the building.
Hence, the velocity of the projectile when it strikes the building is $17.15\,{\text{m/s}}$ in the horizontal direction.

Note: While using equation (2) to determine the vertical component of the final velocity of the projectile, use the vertical component of the initial velocity in the formula instead of resultant initial velocity of the projectile.