Question

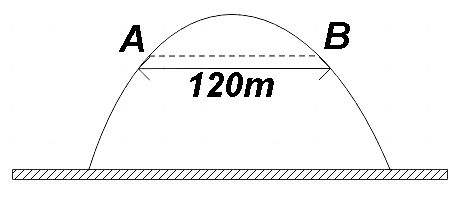
A projectile passes two points A and B at the same heights after 2s and 6s of its projection. The horizontal separation between points A and B is 120m. The horizontal range is closest to $\left( g=10m/{{s}^{2}} \right)$

A. 280m
B. 240m
C. 300m
D.360m

Answer 1

We are given the time taken for the projectile to reach points A and B. From that, we could find the time taken for it to cover the distance of 120m between A and B and hence the horizontal velocity of the projectile. Now find the time of flight of the projectile. The product of the time of flight and horizontal velocity gives you the horizontal range.
Formula used:
Velocity,
$v=\dfrac{x}{t}$

Complete step-by-step solution
In the question, we are given two points A and B on the trajectory of a projectile. The given two points are also at the same heights and also they are separated at a distance of 120m. We are also given acceleration due to gravity as $g=10m{{s}^{-2}}$. Using all this information, we are asked to find the closest value of the horizontal range of the given projectile.
We are said that the time taken for the projectile to reach point B is 6 seconds and the time taken to reach point A is 2 seconds. So the time taken by the projectile to travel from point A to point B would be 4 seconds. So now we could find the horizontal velocity of the projectile as,
${{v}_{x}}=\dfrac{x}{t}$
$\Rightarrow {{v}_{x}}=\dfrac{120m}{4\operatorname{s}}$
$\therefore {{v}_{x}}=30m{{s}^{-1}}$ ………………………… (1)
Now we have the time taken by projectile to complete the rest of the journey from point B as 2 seconds.
So we could say that the time of flight of the projectile will be,
$T=8\sec$ ……………………………………. (2)
Now we know that the product of the time of flight and the horizontal velocity will give us the value of the horizontal range. Therefore the horizontal range of the projectile (R) is given by,
$R={{v}_{x}}\times T$
$\Rightarrow R= 30\times 8$
$\therefore R= 240m$
Therefore we found the value of the horizontal range to be 240m.
Hence, option B is the correct answer.

Note: The range of a projectile is actually the total horizontal distance covered at the end of a projectile motion. The only acceleration acting on a body undergoing projectile motion is the acceleration due to gravity g in the downward direction. Also, for a projectile motion, the horizontal velocity remains constant throughout its motion.