Solveeit Logo
Login

Question

Question: A projectile of mass m is fired with velocity v from a point P at \( \theta =45{}^\circ \). Neglecti...

A projectile of mass m is fired with velocity v from a point P at θ=45∘\theta =45{}^\circ. Neglecting air friction, the magnitude of change of momentum between the leaving point P and arriving point Q is
A. mv2\dfrac{mv}{\sqrt{2}}
B. 2mv2mv
C. 12mv\dfrac{1}{2}mv
D. 2mv\sqrt{2}mv

Explanation

Solution

Recall the expression for change in linear momentum. Remember that the mass and velocity in the horizontal direction remains constant throughout the motion. However the vertical component of velocity will undergo change in a projectile motion. Now find the change in linear momentum using these facts.

Formula used:
Expression for momentum P,
P=mvP=mv

Complete step-by-step answer:
We are firing a mass m at a velocity v and angle 45∘45{}^\circ and we are asked to find the change in momentum between the points: one at which the mass is fired P and the other point Q at which it arrives.
From the Impulse-momentum theorem, we know that the change in momentum is equivalent to the impulse. So by finding the magnitude of change in momentum, we are actually finding the magnitude of impulse.

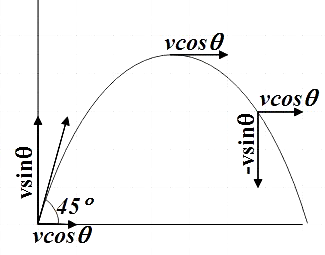
For a projectile motion, we know that the horizontal component of velocity remains constant throughout the motion. However the vertical velocity changes from vsin⁡θj^v\sin \theta \widehat{j} to −vsin⁡θj^-v\sin \theta \widehat{j}
The horizontal component of velocity v is given by, vcos⁡θv\cos \theta
But θ=45∘\theta =45{}^\circ so horizontal component becomes,
vcos⁡θi^=vcos⁡45∘i^=v2i^v\cos \theta \widehat{i}=v\cos 45{}^\circ \widehat{i}=\dfrac{v}{\sqrt{2}}\widehat{i}
Vertical component at the leaving point,
vsin⁡θj^=vsin⁡45∘j^=v2j^v\sin \theta \widehat{j}=v\sin 45{}^\circ \widehat{j}=\dfrac{v}{\sqrt{2}}\widehat{j}
Vertical component at the arriving point,
−vsin⁡θj^=−vsin⁡45∘j^=−v2j^-v\sin \theta \widehat{j}=-v\sin 45{}^\circ \widehat{j}=-\dfrac{v}{\sqrt{2}}\widehat{j}
Change in momentum ΔP\Delta P is given by,
ΔP=Pf−Pi\Delta P={{P}_{f}}-{{P}_{i}}
⇒ΔP=m(vf−vi)\Rightarrow \Delta P=m\left( {{v}_{f}}-{{v}_{i}} \right)
⇒ΔP=m((v2i^−v2j^)−(v2i^+v2j^))\Rightarrow \Delta P=m\left( \left( \dfrac{v}{\sqrt{2}}\widehat{i}-\dfrac{v}{\sqrt{2}}\widehat{j} \right)-\left( \dfrac{v}{\sqrt{2}}\widehat{i}+\dfrac{v}{\sqrt{2}}\widehat{j} \right) \right)
⇒ΔP=−2mv2j^=−2mvj^\Rightarrow \Delta P=-2m\dfrac{v}{\sqrt{2}}\widehat{j}=-\sqrt{2}mv\widehat{j}
But we are asked the magnitude of change in momentum,
∣ΔP∣=2mv\left| \Delta P \right|=\sqrt{2}mv

So, the correct answer is “Option d”.

Note: For a projectile motion when air resistance is negligible, we see that momentum is conserved along the horizontal direction which may otherwise imply that the horizontal forces are zero and the momentum is unchanged. But the net force along the vertical direction is no zero. Hence the momentum is not conserved along the vertical direction.