Question
Question: A projectile is projected with velocity of 40 m/s at an angle $\theta$ with the horizontal. If $R$ b...
A projectile is projected with velocity of 40 m/s at an angle θ with the horizontal. If R be the horizontal range covered by the projectile and after t seconds, its inclination with horizontal becomes zero, then the value of cotθ is [Take, g=10 m/s2]
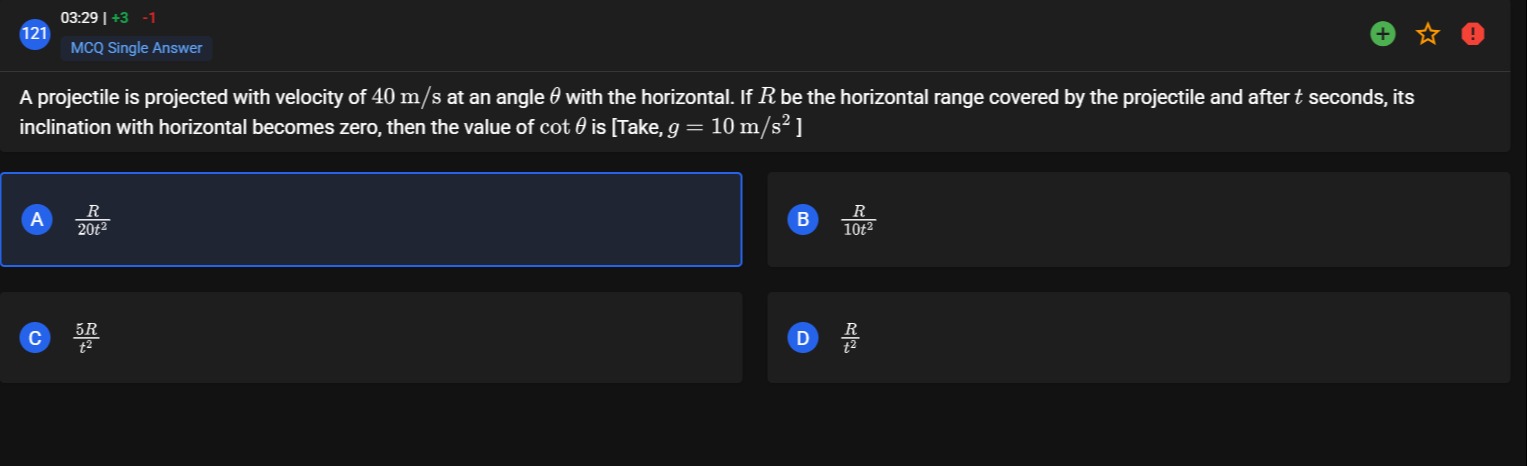
20t2R
10t2R
t25R
t2R
20t2R
Solution
The projectile is projected with an initial velocity u=40 m/s at an angle θ with the horizontal.
The velocity components are ux=ucosθ=40cosθ and uy=usinθ=40sinθ.
The acceleration due to gravity is g=10 m/s2 downwards.
The inclination of the projectile with the horizontal becomes zero at the highest point of its trajectory. The vertical component of velocity is zero at this point.
Let t be the time taken to reach the highest point. The vertical velocity at time t is given by vy(t)=uy−gt.
At t, vy(t)=0.
So, 0=usinθ−gt
usinθ=gt
Substituting u=40 and g=10:
40sinθ=10t
sinθ=4010t=4t (Equation 1)
The horizontal range R is the horizontal distance covered by the projectile when it returns to the initial height. The time taken for this is the total time of flight, which is twice the time taken to reach the highest point.
Total time of flight T=2t.
The horizontal range is given by R=ux×T.
R=(ucosθ)×(2t)
Substituting u=40:
R=(40cosθ)×(2t)
R=80tcosθ (Equation 2)
We need to find the value of cotθ. We know that cotθ=sinθcosθ.
From Equation 1, we have sinθ=4t.
From Equation 2, we have cosθ=80tR.
Now, we can find cotθ:
cotθ=sinθcosθ=4t80tR
cotθ=80tR×t4
cotθ=80t24R
cotθ=20t2R
