Solveeit Logo
Login

Question

Question: A projectile is fixed at an angle \(\theta \) with the horizontal, (as shown in the figure), conditi...

A projectile is fixed at an angle θ\theta with the horizontal, (as shown in the figure), condition under which it lands perpendicular on an inclined plane of inclination α\alpha is?

A. sin⁡ α = cos⁡(θ−α)\sin \,\alpha \, = \,\cos (\theta - \alpha )
B. cos⁡ α = sin⁡(θ−α)\cos \,\alpha \, = \,\sin (\theta - \alpha )
C. 2tan⁡ α = cot⁡(θ−α)2\tan \,\alpha \, = \,\cot (\theta - \alpha )
D. cot⁡(θ−α) = sin⁡ α\cot (\theta - \alpha )\, = \,\sin \,\alpha

Explanation

Solution

Let us understand about the projectile motion. The motion experienced by a propelled target is known as projectile motion. Ballistics is a branch of dynamics that studies the movement, actions, and effects of projectiles, such as bullets, unguided explosives, rockets, and the like; it is also the science or art of designing and accelerating projectiles to achieve a desired result.

Complete step by step answer:

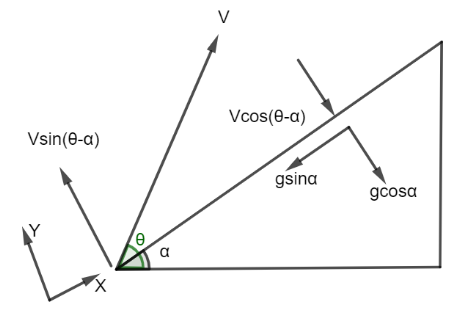
The time of flight (T) is calculated by looking at motion in the y-axis (which is no more vertical as in the normal case). The y-direction displacement after the projectile has returned to the incline, on the other hand, is zero, as it is in the usual case.For y=0y = 0, use the equation of motion perpendicular to the incline.
y=vy×T+12×ayT2=0y = {v_y} \times T + \dfrac{1}{2} \times {a_y}{T^2} = 0
⇒ vsin⁡(θ−α)T+12(−gcos⁡α)T2=0\Rightarrow \,v\sin (\theta - \alpha )T + \dfrac{1}{2}( - g\cos \alpha ){T^2} = 0
\Rightarrow T\left\\{ {\,v\sin (\theta - \alpha ) + \dfrac{1}{2}( - g\cos \alpha )T} \right\\} = 0
Either,T=0,T = 0,
⇒T=2vsin⁡(θ−α)gcos⁡α\Rightarrow T = \dfrac{{2v\sin (\theta - \alpha )}}{{g\cos \alpha }}
Time is given as,
v=u+atv = u + at
⇒0=v cos⁡(θ−α)−(g sin⁡α)t\Rightarrow 0 = v\,\cos (\theta - \alpha ) - (g\,\sin \alpha )t
⇒t=vcos⁡(θ−α)gcos⁡α\Rightarrow t = \dfrac{{v\cos (\theta - \alpha )}}{{g\cos \alpha }}
As we know that the both times are equal so, it can be written as,
vcos⁡(θ−α)gcos⁡α=2vsin⁡(θ−α)gcos⁡α\dfrac{{v\cos (\theta - \alpha )}}{{g\cos \alpha }} = \dfrac{{2v\sin (\theta - \alpha )}}{{g\cos \alpha }}
∴cot⁡(θ−α)=2tan⁡α\therefore \cot (\theta - \alpha ) = 2\tan \alpha

Hence, option C is correct.

Note: Let us know about a special case of trajectory. A lofted trajectory, or one with an apogee greater than the minimum-energy trajectory to the same height, is a special case of a ballistic trajectory for a rocket. To put it another way, the rocket flies higher and hence expends more energy to reach the same landing spot. This can be achieved for a variety of purposes, including raising the distance to the horizon to increase viewing/communication range or adjusting the angle at which a missile can land. In both missile rocketry and spaceflight, lofted trajectories are occasionally used.