Question

A projectile is fired with velocity v at an angle $\theta$ with horizontal. What would be the radius of curvature of path at the instant when magnitude of rate of change of speed of projectile is minimum
$\left( A \right)\dfrac{{{v^2}{{\cos }^2}\theta }}{g}$
$\left( B \right)\dfrac{{{v^2}}}{{g\cos \theta }}$
$\left( C \right)\dfrac{{{v^2}\cos \theta }}{g}$

Answer 1

First we have to draw a rough diagram to get a brief view. Now as the rate of change of speed is minimum the trajectory of the projectile will be at its highest point. Now at that point equate the gravitational force with the centrifugal force of the particle at the highest point.

Complete answer:
As per the problem we know that a projectile is fired with velocity v at an angle $\theta$ with horizontal.
We need to calculate the radius of curvature of the path at the instant when the magnitude of rate of change of speed of projectile is minimum.

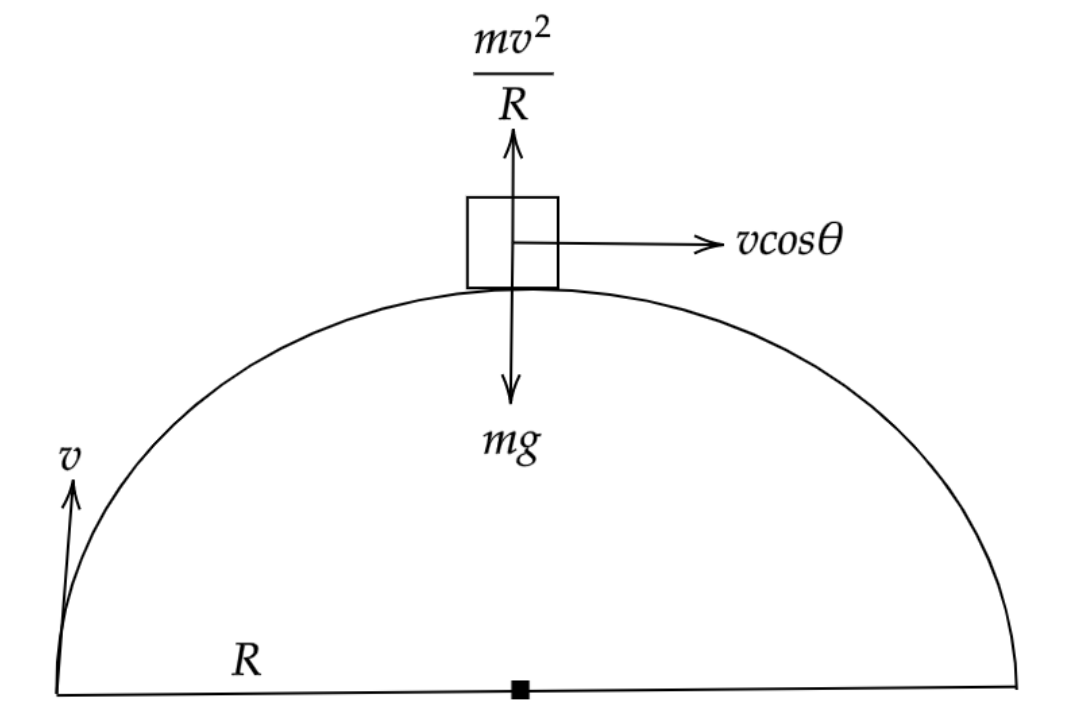
A projectile have a minimum speed at the highest point of its tractorory and this is because the horizontal speed of the projectile motion always remain constant and the only force exert on the projectile is the force due to gravity on the downward direction and in this case that force due to gravity is balanced by the centrifugal force.
So we can write,
$mg = \dfrac{{m{v^2}}}{R}$
Here,
Mass of the body is m
R is the radius of the curvature
Velocity of the projectile is v
Now,
$mg = \dfrac{{m{v^2}}}{R}$
Cancelling the common terms we will get,
$g = \dfrac{{{v^2}}}{R}$
Where we know the horizontal velocity is constant and the velocity of the projectile is,
$vh = v\cos \theta$
Now putting the value of velocity in equation $\left( 1 \right)$ we will get,
$g = \dfrac{{{{\left( {v\cos \theta } \right)}^2}}}{R}$
Rearranging the equation and opening the bracket we will get,
$R = \dfrac{{{v^2}{{\cos }^2}\theta }}{g}$
Therefore the correct option is $\left( A \right)$ .

Note:
Here we have used a trajectory which is defined as the path that an object having some mass which in motion follows through space as a function of time while projectile. Remember that radius of curvature is the radius of the circular path through which an object travels in a projectile motion.