Question

A projectile is fired with a speed $u$ at an angle $\theta$ with the horizontal. Its speed when is direction of motion makes an angle $\alpha$ with the horizontal is
(A). $u\sec \theta \cos \alpha$
(B). $u\sec \theta \sin \alpha$
(C). $u\cos \theta \sec \alpha$
(D). $u\sin \theta \sec \alpha$

Answer 1

A particle follows a projectile under the acceleration of gravity. We can resolve the velocity into its horizontal and vertical components. The horizontal component will remain constant throughout the motion as no acceleration is acting on it in the horizontal direction. At the point where the velocity of the particle makes $\alpha$, we can use trigonometric ratios and components to calculate the magnitude of velocity.

Formulas used:
$\cos \alpha =\dfrac{u\cos \theta }{u'}$

Complete step-by-step solution:
When a particle is thrown at an angle with the horizontal, the motion is called projectile motion. It follows a parabola.
Let the particle make angle $\alpha$ with the horizontal at point P.

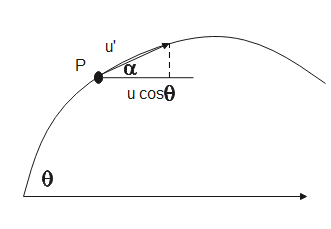
At the starting point, the initial velocity of the particle can be resolved into its components of which the horizontal component remains constant equal to $u\cos \theta$
At point P,
$\cos \alpha =\dfrac{u\cos \theta }{u'}$
Let $u'$ be the velocity at point P, therefore, from the above equation, we get,
$\begin{aligned} & \cos \alpha =\dfrac{u\cos \theta }{u'} \\\ & \Rightarrow u'=\dfrac{u\cos \theta }{\cos \alpha } \\\ & \therefore u'=u\sec \alpha \cos \theta \\\ \end{aligned}$
Therefore, the velocity of the particle at the point where it makes $\alpha$ with the horizontal is $u\sec \alpha \cos \theta$. Hence, the correct option is (C).

Additional information:
As the acceleration of the particle is constant, we can apply equations of motion to calculate the different parameters of projectile motion. The range can be calculated as
$R=\dfrac{{{u}^{2}}\sin 2\theta }{g}$ and the height can be calculated as $\dfrac{{{(u\sin \theta )}^{2}}}{2g}$ and the time taken for the complete motion is $t=\dfrac{u\sin \theta }{g}$.

Note:
At the highest point, $\alpha =0$, $u'=u\cos \theta$ and the vertical component vanishes. In projectile motion, we can analyse the vertical motion and the horizontal motion separately. In the vertical motion, the acceleration due to gravity acts on the particle. At the highest point of the projectile, potential energy is maximum and at the lowest point kinetic energy is maximum.