Question

A projectile is fired at a speed of $100m/s$at an angle of ${{37}^{0}}$above horizontal. At the highest point, the projectile breaks into two parts of mass ratio$1:3$the smaller coming to rest, then the distance between launching point and the point where the heavier piece lands:
A.$480m$
B.$960m$
C.$1120m$
D.$640m$

Answer 1

When projectile reaches the highest point this means its vertical component of velocity becomes zero and its horizontal component of velocity is common through the motion. When a projectile breaks at the highest point the heavy particle follows a new parabolic path because its velocity changes following conservation of momentum because no external forces are acting at the highest point.

Complete answer:

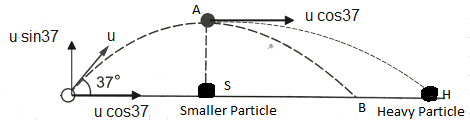
Let us assume the velocity with which projectile is fired as$u=100m/s$
According to question, at highest point $A$projectile breaks into two parts of mass ratio$1:3$and the smaller particle comes at rest so it must fall immediately from highest point A and reach at point S under gravity while heavier particle reaches to point H on new projectile path because its velocity get changed.
Let us assume Mass of heavier part is $3x$
Mass of lighter part is $x$
Since at point A all external forces are zero so momentum is conserved.
Let us assume the velocity of heavier particles at point A will be ${{v}_{h}}$and that of lighter particles is ${{v}_{l}}$ .
According to conservation of momentum,
$(4x)(100cos{{37}^{0}})=(3x)({{v}_{h}})+(x)({{v}_{l}})$
$(4x)(76.5)=(3x)({{v}_{h}})+(x)(0)$
${{v}_{h}}=102m{{s}^{-1}}$----Equation (1)
So the velocity of the heavy particle at the highest point will become$102m{{s}^{-1}}$and it will follow a new projectile path and reach at point H.
If projectile does not break at point A then it will reach the ground at point B following the initial projectile path.
So Range of initial projectile path when whole particle is present is calculated as –
$R=\dfrac{2{{u}^{2}}Sin\theta Cos\theta }{g}$
$R=\dfrac{2{{(100)}^{2}}Sin{{37}^{0}}Cos{{37}^{0}}}{9.8}$
$R=980.87m$
Distance of $OB=980.87m$
since S is the midpoint of OB. So we can write $OS=SB=490.44m$--- Equation (2)
Maximum height of Projectile is calculated as –
$H=\dfrac{{{u}^{2}}Si{{n}^{2}}\theta }{2g}$
$H=\dfrac{{{(100Sin37)}^{2}}}{2\times 9.8}$
$H=184.77m$
Now consider only the heavier particle it is performing half projectile motion from the highest point with new velocity$102m{{s}^{-1}}$. (From equation 1)
So time taken by that heavy particle to reach point H from highest point A is calculated as,
$t=\sqrt{\dfrac{2H}{g}}=\sqrt{\dfrac{2\times 184.77}{9.8}}=6.14s$
Horizontal distance SH covered by this heavy particle will be calculated as,
$Dis\tan ce=Speed\times time$
$SH=102\times 6.14=626.28m$----- Equation (3)
We have to calculate the distance between launching point and point where the heavier particle lands.
Let us assume that distance to OH.
$OH=OS+SH$
Put the values of OS and SH from Equation 2 and Equation 3 respectively.
$OH=490.44+626.28$
OH=1116.72m$$$$\approx 1120m.

So,option C is the correct answer.

Note:
When no external force acts on the system then momentum of the system remains conserved, which signifies that initial momentum is equal to final momentum. Whenever projectile motion particles break and velocity of particles gets changed then that particles will always follow a new parabolic path and their velocity can be calculated by using the Law of conservation of momentum because no external force acts on the system.