Question

A projectile has the maximum range of 500m. If the projectile is thrown up at an incline plane of ${30^ \circ }$ with the same velocity, the distance covered by it along the inclined plane is:
a. 250m
b. 500m
c. 400m
d. 1000m

Answer 1

A projectile motion is the motion when an object is thrown at some angle from horizontal and the motion is in two dimensions then this type of the motion is known as projectile motion and the path travelled by the object is called the trajectory. Maximum range is the total horizontal distance that the object travels.

Formula used:
The formula of the rage is given by,
$\Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}$
Where the range is R the initial velocity is u the angle is $\theta$ the acceleration due to gravity is g.
The formula of the third relation of the Newton’s law of motion is given by,
$\Rightarrow {v^2} - {u^2} = 2as$
Where final velocity is v the initial velocity is u the acceleration is a and the distance travelled is s.
The formula of the acceleration on the inclined plane is given by,
$\Rightarrow a = - g\sin \theta$
Where acceleration on the projectile on the inclined plane is a, the acceleration due to gravity is g and the inclination angle is $\theta$.

Complete step by step answer:
Step1:
The range of a projectile is given by the equation-
$\Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}$
Where u= initial velocity, $\theta$=angle of projection, $g$=acceleration due to gravity

Now for maximum horizontal range $\theta$ is equal to, $\theta$=${45^ \circ }$.
Therefore,
$\Rightarrow {R_{\max }} = \dfrac{{{u^2}}}{g}$.

Step2:
Now substitute the values in above equation to calculate the initial velocity
Therefore,
$\Rightarrow 500 = \dfrac{{{u^2}}}{g}$
$\Rightarrow {u^2} = 500g$
$\Rightarrow u = \sqrt {500g}$………eq. (1)

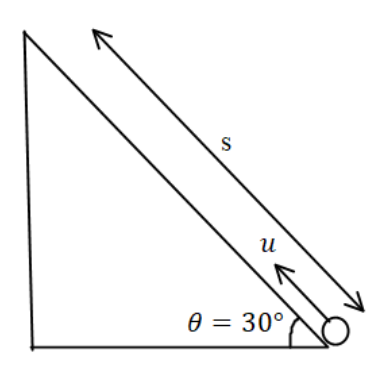
Step3:
Now use the velocity position relation to calculate the distance,
$\Rightarrow {v^2} - {u^2} = 2as$………eq. (2)
Where final velocity is v the initial velocity is u the acceleration is a and the distance travelled is s.
At maximum height v=0 also acceleration along the inclined plane is given by,
$\Rightarrow a = - g\sin {30^ \circ }$
So from eq. (2) substitute all the values
$\Rightarrow 0 - {u^2} = 2( - g\sin {30^ \circ })s$
$\Rightarrow {u^2} = gs$
$\Rightarrow s = \dfrac{{{u^2}}}{g}$
But we have calculated that,
$\Rightarrow \dfrac{{{u^2}}}{g} = 500$
Therefore distance$s = 500m$.

Hence, the correct answer is option (B).

Note: Remember that for a body moving in x-direction, at maximum height its velocity is always zero but it can have some acceleration. For maximum range the value of angle of inclination should be $\theta = 45^\circ$ and if the projectile is thrown up with on the inclined plane then the acceleration in the downwards direction and resisting the motion of the projectile.