Question

A projectile fired from the bottom of an inclined plane strikes the plane with horizontal velocity. If the angle of projection is $\theta$, what will be the angle of the inclined plane with horizontal?
A. ${{\tan }^{-1}}\left( \dfrac{1}{2}\cos \theta \right)$
B. ${{\cos }^{-1}}\left( \dfrac{1}{2}\tan \theta \right)$
C. ${{\tan }^{-1}}\left( 2\sec \theta \right)$
D. ${{\tan }^{-1}}\left( \dfrac{1}{2}\tan \theta \right)$

Answer 1

First, draw a figure to relate the given situation in the question. Then with the help of the expressions for the horizontal range and maximum height and trigonometry, calculate the tangent of the angle of inclination of the plane.

Formula used:
$R=\dfrac{{{u}^{2}}\sin 2\alpha }{g}$
$H=\dfrac{{{u}^{2}}{{\sin }^{2}}\alpha }{2g}$
$T=\dfrac{2u\sin \alpha }{g}$
Here, u is the initial velocity of the projectile, $\alpha$ is the angel of projection, g is acceleration due to gravity, R is the horizontal range, H is the maximum height and T is the time of flight.

Complete step by step answer:
Let the angle of inclination of the inclined plane be $\alpha$. It is given that when the projectile hits the inclined planes (say at point A), it has only horizontal velocity (velocity only in the horizontal direction). Since the vertical velocity of the projectile at point A is zero, this means that the highest or maximum height achieved by the projectile is at point A.
We know that the maximum height of a projectile is given by $H=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}$.

When a projectile reaches the maximum height, the horizontal displacement of the projectile is equal to half of the horizontal range.
i.e. $\dfrac{R}{2}$.
And $R=\dfrac{{{u}^{2}}\sin 2\alpha }{g}$.

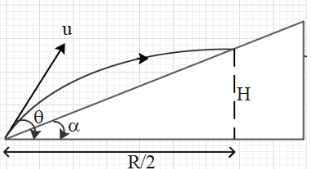
From the figure, we get that $\tan \alpha =\dfrac{H}{\left( \dfrac{R}{2} \right)}$.
Substitute the expressions of H and R in the above equation.
$\tan \alpha =\dfrac{2H}{R}=\dfrac{2\left( \dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g} \right)}{\left( \dfrac{{{u}^{2}}\sin 2\theta }{g} \right)}=\dfrac{{{\sin }^{2}}\theta }{\sin 2\theta }$ …. (i)
Here, we can write $\sin 2\theta =2\sin \theta \cos \theta$.
Substitute this value in (i).
$\Rightarrow \tan \alpha =\dfrac{{{\sin }^{2}}\theta }{2\sin \theta \cos \theta }$
$\Rightarrow \tan \alpha =\dfrac{\sin \theta }{2\cos \theta }$
We know that $\dfrac{\sin \theta }{\cos \theta }=\tan \theta$
Then,
$\therefore\tan \alpha =\dfrac{1}{2}\tan \theta$
With this we get that $\alpha ={{\tan }^{-1}}\left( \dfrac{1}{2}\tan \theta \right)$

Hence, the correct option is D.

Note: If you do not understand why we took the time taken as half of the time of flight then know that the motion of the projectile (in absence of air resistance) is symmetric about an vertical axis passing through the highest point (i.e. A). Therefore, the time taken to the reach A is half of the total time to reach ground. If you do not know the formula for H, R and T you also use the suitable kinematic equations in this question.