Question

A projectile fired at an angle of ${{45}^{0}}$with the horizontal. Elevation angle of the projectile at its highest point as seen from the point of projection is?
$A.\quad {{60}^{0}}$
$B.\quad {{\tan }^{-1}}\dfrac{1}{2}$
$C.\quad {{\tan }^{-1}}(\dfrac{\sqrt{3}}{2})$
$D.\quad {{45}^{0}}$

Answer 1

Hint: Projectile motion of a body initially fired at an angle of $\theta ={{45}^{0}}$with the horizontal is fired. We will then find the maximum height of the projectile: ${{h}_{\max }}=\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}$. The range (R) of the projectile motion is, $R=\dfrac{{{u}^{2}}\sin 2\theta }{g}$. The value of angle of elevation at the highest point, from the point of projection can be found by $\tan \phi$ for the right angled triangle OAB.

Step by step solution:
Let’s start by making a detailed diagram of projectile motion given in the problem.

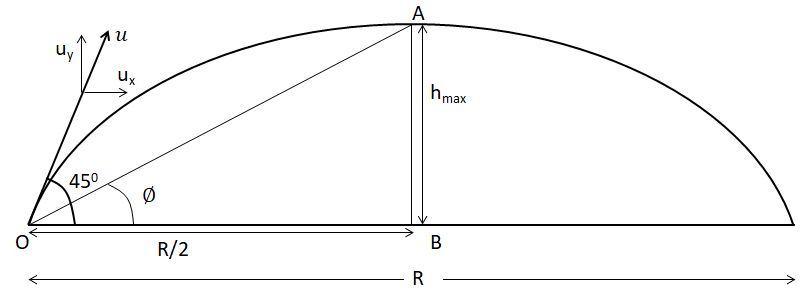
The initial velocity of the projectile is (u) making an angle of $\theta ={{45}^{0}}$with the horizontal. We will break the initial velocity (u) into the horizontal component given by: ${{u}_{x}}=u\sin \theta =u\sin {{45}^{0}}=\dfrac{u}{\sqrt{2}}$. Similarly, the vertical component of the initial velocity (u) is given by: ${{u}_{y}}=u\cos \theta =u\cos {{45}^{0}}=\dfrac{u}{\sqrt{2}}$.
To find the maximum height of the projectile, we will consider the newton’s laws of motion in two dimension: ${{h}_{\max }}=\dfrac{v_{y}^{2}-u_{y}^{2}}{2g}$. At the maximum height of the projectile motion, the final velocity of the body along the vertical will be zero and the acceleration due to gravity will be (-g), since it is against the direction of the motion. Therefore: ${{h}_{\max }}=\dfrac{v_{y}^{2}-u_{y}^{2}}{2g}\Rightarrow {{h}_{\max }}=\dfrac{(0)_{{}}^{2}-(\dfrac{u}{\sqrt{2}})_{{}}^{2}}{2(-g)}\Rightarrow {{h}_{\max }}=\dfrac{{{u}^{2}}}{4g}$.
Similarly, we will find the time of flight of the projectile motion. To find the time (T=2t), we will use the formula: ${{v}_{y}}={{u}_{y}}+(-g)t$. Putting in the initial and final values of the vertical velocity we find: ${{v}_{y}}={{u}_{y}}+(-g)t\Rightarrow 0=\dfrac{u}{\sqrt{2}}-gt\Rightarrow t=\dfrac{u}{g\sqrt{2}}$. Hence, $T=2t=\dfrac{u\sqrt{2}}{g}$
Using this value of the time of flight (t), we will find the horizontal range (R) of the projectile motion, which is the horizontal distance travelled by the projectile.
$\therefore R={{u}_{x}}t+\dfrac{1}{2}a{{T}^{2}}$. However, since no horizontal acceleration acts on the projectile, hence a=0.
Therefore the value of R becomes, $R={{u}_{x}}t+\dfrac{1}{2}a{{T}^{2}}\Rightarrow R=\dfrac{u}{\sqrt{2}}(\dfrac{\sqrt{2}u}{g})+\dfrac{1}{2}(0){{t}^{2}}\Rightarrow R=\dfrac{{{u}^{2}}}{g}$.
The base of the right angled triangle OAB is $\dfrac{R}{2}$, which is: $\dfrac{R}{2}=\dfrac{{{u}^{2}}}{2g}$.
Hence, to find the angle of elevation at the highest point, from the point of projection, we will find$\tan \phi$. That is, $\tan \phi =\dfrac{{{h}_{\max }}}{\dfrac{R}{2}}\Rightarrow \tan \phi =\dfrac{\dfrac{{{u}^{2}}}{4g}}{\dfrac{{{u}^{2}}}{2g}}\Rightarrow \tan \phi =\dfrac{{{u}^{2}}}{4g}\times \dfrac{2g}{{{u}^{2}}}\Rightarrow \tan \phi =\dfrac{1}{2}\Rightarrow \phi ={{\tan }^{-1}}(\dfrac{1}{2})$.
Hence, Option B is the solution.

Note: The value of the total time of flight is given by (T). This value is equal to 2t, because (t) is the amount of time taken by the projectile to reach the maximum height, hence that is half the total time of flight. Upon reaching the highest point, it takes an equal amount of time (t) to reach the ground. Hence, the total time of flight is (T).