Question

A projectile A is thrown at an angle of $30^\circ$ to the horizontal from point P. At the same time, another projectile B is thrown with velocity $v_2$ upwards from the point Q vertically below the highest point. For B to collide with A, $\dfrac{{v_2}}{{v_1}}$ should be

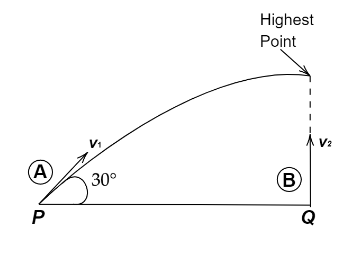
A. $1$
B. $2$
C. $\dfrac{1}{2}$
D. $4$

Answer 1

The projectile A is thrown at an angle hence we will get two compnet after rev;oving. Now as per the problem statement for A and B to collide the vertical velocity of the two particles initial vertical component must be equals so as to meet at a point at a particular time. After solving two step we can get the required ratio.

Complete step by step answer:
As per the given problem a projectile A is thrown at an angle of $30^\circ$ to the horizontal from point P. At the same time, another projectile B is thrown with velocity $v_2$ upwards from the point Q vertically below the highest point.We need to calculate the $\dfrac{{v_2}}{{v_1}}$ if the B collides with A.

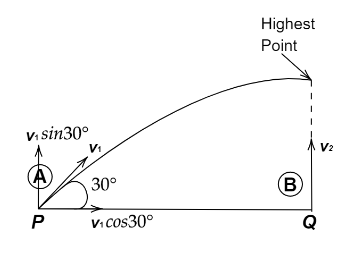
As the A is projected at an angle of $30^\circ$ then the velocity must be slipped into two compnet one is vertical and another is horizontal. $v_1$ is the velocity of A.
$v_1H = v_1\cos 30^\circ$
Where, $v_1H$ is the horizontal component of A.
$v_1V = v_1\sin 30^\circ$
Where, $v_1V$ is the vertical component of B.
And B is thrown with velocity $v_2$ upwards.Hence vertical velocity is the same as the projected velocity.

For A and B to collide , the initial vertical components of the velocities must be equal.
Equation velocities along the vertical we will get,
Vertical velocity of A= Vertical velocity of B
$v_1V = v_2$
Now putting the vertical component of A we will get,
$v_1\sin 30^\circ = v_2$
We know the value of $sin30 = \dfrac{1}{2}$
Now,
$v_1 \times \dfrac{1}{2} = v_2$
Now rearranging the equation we will get,
$\therefore \dfrac{{v_2}}{{v_1}} = \dfrac{1}{2}$

Therefore the correct option is $\left( C \right)$.

Note: When two or more bodies collide then an event called collision takes place where these bodies exert force on each other in a short period of time. Remember that the horizontal component remains the same throughout the flight and hence the horizontal motion of a projectile is independent of its vertical motion.