Question
Question: A prismatic bar of a given dimension is kept in water. Find the hydrostatic forces on the slant face...
A prismatic bar of a given dimension is kept in water. Find the hydrostatic forces on the slant face.
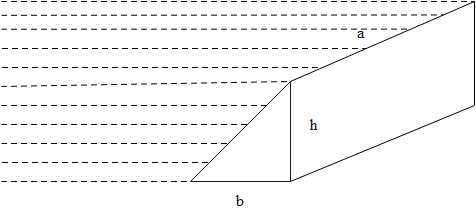
Solution
The pressure of a fluid exerts a force on the surface which comes in contact with the fluid. The force that gets distributed over the area will have the resultant magnitude and the direction. Thus, the force will be the product of pressure and area.
Formula used:
F=P×A
Complete answer:
The pressure of a fluid exerts a force on the surface which comes in contact with the fluid. The force that gets distributed over the area will have the resultant magnitude and the direction.
The pressure of a fluid exerts thrust on each part of a surface with which the fluid made contact. Each force distributed over the area has a resultant magnitude and direction that is very crucial. In the case of a horizontal surface, over the plane, the pressure does not vary. So, the total force will be the product of the pressure and the area and its direction will be perpendicular to the plane. In the case of a surface that is not horizontal, the pressure will vary at each point of the surface. So, the calculation of the total thrust will be different.
