Question
Question: A prism shaped imaginary structure is given. A point charge is kept as given in figure. Calculate th...
A prism shaped imaginary structure is given. A point charge is kept as given in figure. Calculate the electric flux passing through the prism.
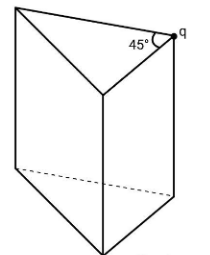
(A) 4ε0q
(B) 8ε0q
(C) 16ε0q
(D) 32ε0q
Solution
Here, you are given a prism which is imaginary and an electric charge is placed at the corner of the prism. You are asked to find the electric flux passing through the prism. Now, this question may seem tough that is too hard to solve because whenever you are asked to find the electric flux through a closed surface, the first thing that comes to your mind is the Gauss’s law and you apply that. But Gauss’s law is easy to work out for the shape of surfaces that are symmetric. Here, the surface with respect to the electric charge is not symmetric and hence it will be tough to apply Gauss’s law, that is what it seems to be. But you can use a trick here and then simply apply the Gauss’s law. The trick also involves symmetry and you need to figure out what can be done in order to solve this question easily.
Complete step by step answer:
Gauss's law states that the electric flux through a closed surface is equal to the charge enclosed within that closed surface divided by the permittivity of the medium.Mathematically, we have Gauss’s law given by Φ=∮E.dA=ε0qenc, where E is the electric field vector, dA is the infinitesimally small area on the surface, qenc is the charge enclosed and ε0v is the permittivity in vacuum.
Now, let us come back to our question. Here, you are given a prism. This prism can be considered as a part of a cube. Actually, this prism will be the 16th part of a cube. If you take 16 prisms similar to the given prism and place it appropriately, you will complete a cube. Now, the centre of this cube will be the electric charge. Try to imagine. Now, you can apply Gauss's law. The flux through the cube will be given as Φ=ε0q. Because the charge enclosed in the cube is equal to q and it is placed at the centre.
Now, due to symmetry, the flux will flow equally through all the prisms. There are a total of 16 prisms out of which 8 are below and 8 are above. Therefore, the flux ε0q will be equally divided into 16 prisms and flux through each prism will be 16ε0q.Therefore, the electric flux passing through the prism will be equal to 16ε0q.
Hence, option C is correct.
Note: We have used a crucial trick of considering the prism as a part of a cube. Also, we have used the concept of symmetry that due to symmetry the electric flux through each prism will be equal. Remember Gauss’s law which states that the electric flux through a closed surface is proportional to the charge enclosed by the surface.
