Question

A prism of the refractive index $\sqrt{2}$ has a refracting angle $60{}^\circ$ . So that a ray suffers minimum deviation it should be incident at an angle:
A. $45{}^\circ$
B. $90{}^\circ$
C. $30{}^\circ$
D. none

Answer 1

The angle of the triangle of a prism which is between the two sides through which the refracted ray passes by is known as the refracting angle. It is denoted by $A$. When there is a minimum deviation the angle of incidence is equivalent to the angle of emergence.

Complete step-by-step answer:
The angle of deviation is the angle between the incident ray and the emergent ray. It is denoted by $\delta$. It depends on the refractive index and the refracting angle of the prism.
Mathematically,
$\delta =\left( \mu -1 \right)A$
The angle of incidence is given as,
$i=\dfrac{A+{{\delta }_{m}}}{2}$

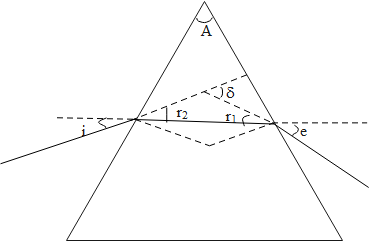
In the case of minimum deviation, both the angle of refraction is equal,
${{r}_{1}}={{r}_{2}}$
As the refracting angle is equal to the sum of the refractive angle of the prism. So the angle of refraction in case of minimum deviation will be,
$\begin{aligned} & A={{r}_{1}}+{{r}_{2}} \\\ & \Rightarrow A=2r \\\ & \Rightarrow r=\dfrac{A}{2} \\\ & \Rightarrow r=\dfrac{60}{2}=30{}^\circ \\\ \end{aligned}$
According to Snell’s law, the refractive index of a prism is given as the ratio of the angle of incidence and the angle of refraction of the prism.
Mathematically,
$\mu =\dfrac{\sin i}{\sin r}$
So, by putting the values as per the information provided in the question:
$\begin{aligned} & \sqrt{2}=\dfrac{\sin i}{\sin 30{}^\circ } \\\ & \Rightarrow \sin i=\sqrt{2}\sin 30{}^\circ \\\ & \Rightarrow \sin i=\dfrac{\sqrt{2}}{2}=\dfrac{1}{\sqrt{2}} \\\ & \Rightarrow {{\sin }^{-1}}\dfrac{1}{\sqrt{2}}=45{}^\circ \\\ & \therefore \angle i=45{}^\circ \\\ \end{aligned}$

So, the correct answer is “Option A”.

Note: Snell’s law was discovered by mathematician Willebrord Snell in the year 1621. In his law, he gave a relation be the angle of incidence, angle of refraction, and the refractive angle of the light beam which is passing through different mediums. In the case of minimum deviation, the incidence angle is the same as that of the angle of emergence and the deviation angle is the least.