Question

A prism of refractive index 1.53 is placed in water of refractive index 1.33. If the angle of the prism is $60^\circ$, calculate the angle of minimum deviation in water.

Answer 1

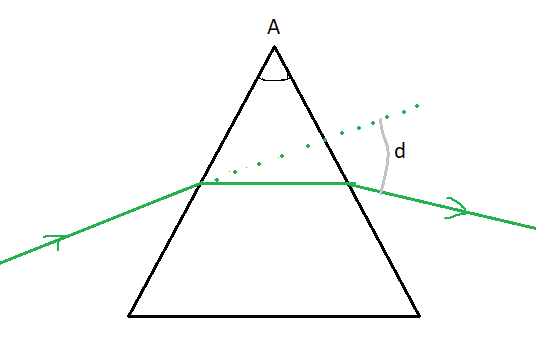
The angle of deviation ($\delta$) depends upon the angle of incidence, if the angle of incidence of the light increases, the angle of deviation (δm) decreases till it becomes minimum at a particular angle of incidence. The minimum value of the angle of deviation is called the angle of minimum deviation ($\delta_m$).

Complete step by step answer:
According to question we have,
Angle of prism($A$) = $60^\circ$
Refractive index of glass $\mu_g$ = 1.53
(Because prism is made up of glass that is why we write refractive index of glass)
Refractive index of water $\mu_w$ = 1.33
Now, the refractive index (n) = $\dfrac{{{\mu _g}}}{{{\mu _w}}}$

$\Rightarrow n = \dfrac{{1.53}}{{1.33}} = 1.15$
Now we apply the prism formula to find the minimum angle of deviation (δm).
$n = \dfrac{{\sin [(A + {\delta _m})/2]}}{{\sin (A/2)}}$
$\Rightarrow 1.15 = \dfrac{{\sin [(60^\circ + {\delta _m})/2]}}{{\sin (60^\circ /2)}}$
$\Rightarrow \dfrac{{{\text{60}}^\circ {\text{ + }}{\delta _{\text{m}}}}}{2} = {\sin ^{ - 1}}\left( {1.15 \times \sin \dfrac{{60^\circ }}{2}} \right)$
$\Rightarrow \dfrac{{{\text{60}}^\circ {\text{ + }}{\delta _{\text{m}}}}}{2} = {\sin ^{ - 1}}\left( {1.15 \times \sin 30^\circ } \right)$
$\Rightarrow \dfrac{{{\text{60}}^\circ {\text{ + }}{\delta _{\text{m}}}}}{2} = {\sin ^{ - 1}}\left( {1.15 \times \dfrac{1}{2}} \right)$ $\because \left( {\sin 30^\circ = \dfrac{1}{2}} \right)$
$\Rightarrow \dfrac{{{\text{60}}^\circ {\text{ + }}{\delta _{\text{m}}}}}{2} = {\sin ^{ - 1}}\left( {0.575} \right) = 35.1^\circ$
$\Rightarrow 60^\circ + {\delta _m} = 35.1^\circ \times 2$
$\therefore {\delta _m} = 70.2^\circ - 60^\circ = 10.2^\circ$

Therefore the angle of minimum deviation in water $({\delta _m}) = 10.2^\circ$

Additional information:
There is a necessary condition for the minimum deviation, the prism lies symmetrically with respect to the incident ray and the emergent ray i.e.($i=e$). The angle between the emergent ray and the direction of the incident ray is called the angle of deviation. There is one and only one angle of incidence for which the deviation produced by the prism is minimum. For any other angle of deviation, there are two values of ($i$) and ($e$).

Note:
The angle of minimum deviation (\delta_m) is also denoted by( $D_m$). Deviation produced by a very thin prism does not depend upon the angle of incidence i.e., it is a constant quantity for a given prism. A thin prism gives deviation of light.