Question
Question: A prism of prism angle $(A=60^\circ)$ and refractive index $n_2$ is placed in a liquid of refractive...
A prism of prism angle (A=60∘) and refractive index n2 is placed in a liquid of refractive index n1. A light ray is incident on face AB at constant angle of incidence i and it emerges at surface AC at angle of emergent e. Somehow n1 is increasing at rate N1 and n2 is increasing at rate N2. Choose the correct option(s)
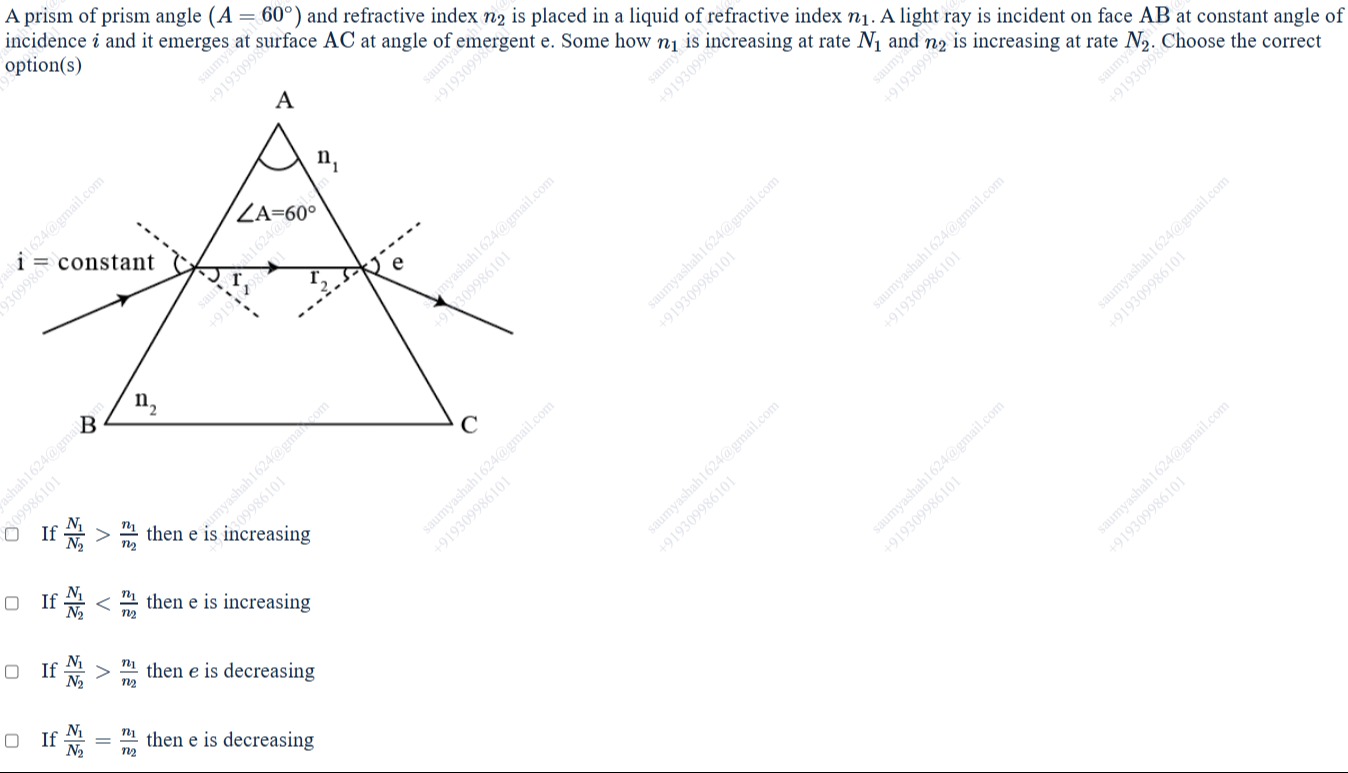
If N2N1>n2n1 then e is increasing
If N2N1<n2n1 then e is increasing
If N2N1>n2n1 then e is decreasing
If N2N1=n2n1 then e is decreasing
Options 2 and 3
Solution
We start with the two refraction conditions:
-
At the first face (AB): n1sini=n2sinr1
-
At the second face (AC): n2sinr2=n1sine
Also, by geometry inside the prism: r1+r2=A (with A=60∘)
Since the angle of incidence i is fixed, differentiate equation (1) with respect to time t: n1sini=n2sinr1
Differentiating (with i constant) gives: 0=n2cosr1(dr1/dt)
More precisely, cosr1(dr1/dt)=sini⋅[(d(n1)/dt⋅n2–n1⋅d(n2)/dt]/n22
Similarly, differentiating (2) and using r2=A–r1, one eventually finds that cose(de/dt)=(N2n1–n2N1)⋅[positivefactors].
All the trigonometric factors (like sin(A−r1), cose, cosr1, etc.) are positive in the allowed range. Thus the sign of de/dt is determined by the factor (N2n1–n2N1). In other words,
de/dt>0 if N2n1–n2N1>0⟹N1/N2<n1/n2,
de/dt<0 if N2n1–n2N1<0⟹N1/N2>n1/n2.
Thus we conclude:
- If (N1/N2)<(n1/n2) then the emergent angle e is increasing.
- If (N1/N2)>(n1/n2) then the emergent angle e is decreasing.
