Solveeit Logo
Login

Question

Question: A prism is made of wire mesh with each side having equal resistance R. A battery of 30V and zero int...

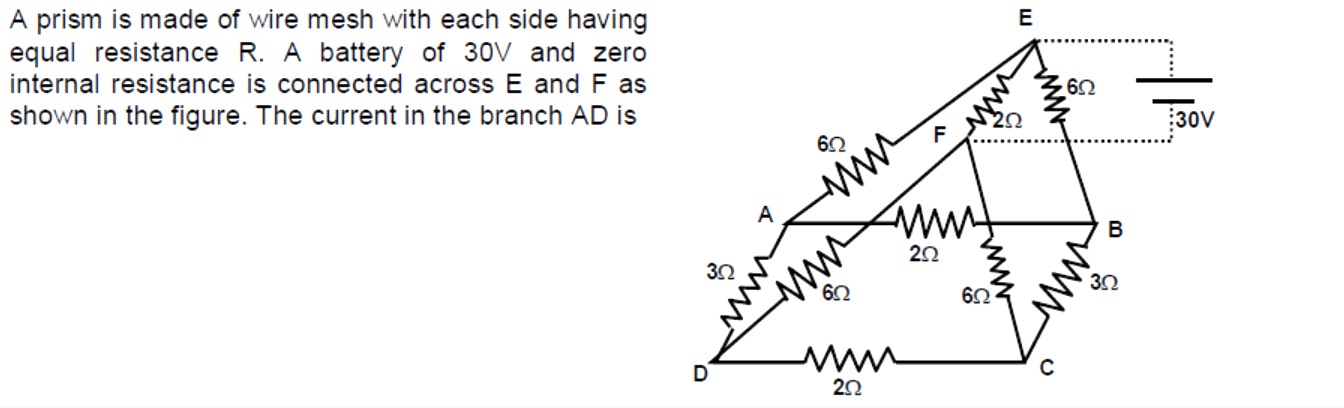
A prism is made of wire mesh with each side having equal resistance R. A battery of 30V and zero internal resistance is connected across E and F as shown in the figure. The current in the branch AD is

Answer

10/39 A

Explanation

Solution

The problem asks for the current in the branch AD of a given resistor network, which is shaped like a prism. A battery of 30V is connected across points E and F.

First, let's clarify the resistance values. The problem statement says "each side having equal resistance R", but the figure shows specific, different resistance values (2Ω, 3Ω, 6Ω) for various branches. In such cases, the specific values given in the diagram override the generic statement. We will use the resistance values shown in the figure.

Let's list the nodes and their connections with resistances:

  • Battery connected across E and F, so let V_F = 0V and V_E = 30V.
  • The other nodes are A, B, C, D. Let their potentials be V_A, V_B, V_C, V_D.
  • The resistances are:
    • R_EA = 6Ω
    • R_EB = 6Ω
    • R_FA = 2Ω
    • R_FB = 6Ω
    • R_AB = 2Ω
    • R_AD = 3Ω
    • R_BC = 3Ω
    • R_CD = 2Ω
    • R_AC = 6Ω
    • R_BD = 6Ω

We will use Kirchhoff's Current Law (KCL) at each unknown node (A, B, C, D).

1. KCL at Node A: Currents leaving node A sum to zero: VA−VEREA+VA−VFRFA+VA−VBRAB+VA−VCRAC+VA−VDRAD=0\frac{V_A - V_E}{R_{EA}} + \frac{V_A - V_F}{R_{FA}} + \frac{V_A - V_B}{R_{AB}} + \frac{V_A - V_C}{R_{AC}} + \frac{V_A - V_D}{R_{AD}} = 0 VA−306+VA−02+VA−VB2+VA−VC6+VA−VD3=0\frac{V_A - 30}{6} + \frac{V_A - 0}{2} + \frac{V_A - V_B}{2} + \frac{V_A - V_C}{6} + \frac{V_A - V_D}{3} = 0 Multiply by 6: (VA−30)+3VA+3(VA−VB)+(VA−VC)+2(VA−VD)=0(V_A - 30) + 3V_A + 3(V_A - V_B) + (V_A - V_C) + 2(V_A - V_D) = 0 VA−30+3VA+3VA−3VB+VA−VC+2VA−2VD=0V_A - 30 + 3V_A + 3V_A - 3V_B + V_A - V_C + 2V_A - 2V_D = 0 10VA−3VB−VC−2VD=30(1)10V_A - 3V_B - V_C - 2V_D = 30 \quad (1)

2. KCL at Node B: VB−VEREB+VB−VFRFB+VB−VARAB+VB−VCRBC+VB−VDRBD=0\frac{V_B - V_E}{R_{EB}} + \frac{V_B - V_F}{R_{FB}} + \frac{V_B - V_A}{R_{AB}} + \frac{V_B - V_C}{R_{BC}} + \frac{V_B - V_D}{R_{BD}} = 0 VB−306+VB−06+VB−VA2+VB−VC3+VB−VD6=0\frac{V_B - 30}{6} + \frac{V_B - 0}{6} + \frac{V_B - V_A}{2} + \frac{V_B - V_C}{3} + \frac{V_B - V_D}{6} = 0 Multiply by 6: (VB−30)+VB+3(VB−VA)+2(VB−VC)+(VB−VD)=0(V_B - 30) + V_B + 3(V_B - V_A) + 2(V_B - V_C) + (V_B - V_D) = 0 VB−30+VB+3VB−3VA+2VB−2VC+VB−VD=0V_B - 30 + V_B + 3V_B - 3V_A + 2V_B - 2V_C + V_B - V_D = 0 −3VA+8VB−2VC−VD=30(2)-3V_A + 8V_B - 2V_C - V_D = 30 \quad (2)

3. KCL at Node C: VC−VARAC+VC−VBRBC+VC−VDRCD=0\frac{V_C - V_A}{R_{AC}} + \frac{V_C - V_B}{R_{BC}} + \frac{V_C - V_D}{R_{CD}} = 0 VC−VA6+VC−VB3+VC−VD2=0\frac{V_C - V_A}{6} + \frac{V_C - V_B}{3} + \frac{V_C - V_D}{2} = 0 Multiply by 6: (VC−VA)+2(VC−VB)+3(VC−VD)=0(V_C - V_A) + 2(V_C - V_B) + 3(V_C - V_D) = 0 VC−VA+2VC−2VB+3VC−3VD=0V_C - V_A + 2V_C - 2V_B + 3V_C - 3V_D = 0 −VA−2VB+6VC−3VD=0(3)-V_A - 2V_B + 6V_C - 3V_D = 0 \quad (3)

4. KCL at Node D: VD−VARAD+VD−VBRBD+VD−VCRCD=0\frac{V_D - V_A}{R_{AD}} + \frac{V_D - V_B}{R_{BD}} + \frac{V_D - V_C}{R_{CD}} = 0 VD−VA3+VD−VB6+VD−VC2=0\frac{V_D - V_A}{3} + \frac{V_D - V_B}{6} + \frac{V_D - V_C}{2} = 0 Multiply by 6: 2(VD−VA)+(VD−VB)+3(VD−VC)=02(V_D - V_A) + (V_D - V_B) + 3(V_D - V_C) = 0 2VD−2VA+VD−VB+3VD−3VC=02V_D - 2V_A + V_D - V_B + 3V_D - 3V_C = 0 −2VA−VB−3VC+6VD=0(4)-2V_A - V_B - 3V_C + 6V_D = 0 \quad (4)

Now we solve the system of four linear equations (1), (2), (3), (4) for V_A, V_B, V_C, V_D.

From (3), VA=−2VB+6VC−3VD(3a)V_A = -2V_B + 6V_C - 3V_D \quad (3a) From (4), 2VA+VB+3VC−6VD=0(4a)2V_A + V_B + 3V_C - 6V_D = 0 \quad (4a)

Substitute (3a) into (4a): 2(−2VB+6VC−3VD)+VB+3VC−6VD=02(-2V_B + 6V_C - 3V_D) + V_B + 3V_C - 6V_D = 0 −4VB+12VC−6VD+VB+3VC−6VD=0-4V_B + 12V_C - 6V_D + V_B + 3V_C - 6V_D = 0 −3VB+15VC−12VD=0-3V_B + 15V_C - 12V_D = 0 Divide by -3: VB−5VC+4VD=0  ⟹  VB=5VC−4VD(5)V_B - 5V_C + 4V_D = 0 \implies V_B = 5V_C - 4V_D \quad (5)

Substitute (5) into (3a): VA=−2(5VC−4VD)+6VC−3VDV_A = -2(5V_C - 4V_D) + 6V_C - 3V_D VA=−10VC+8VD+6VC−3VDV_A = -10V_C + 8V_D + 6V_C - 3V_D VA=−4VC+5VD(6)V_A = -4V_C + 5V_D \quad (6)

Now substitute (5) and (6) into (1) and (2):

Substitute into (1): 10(−4VC+5VD)−3(5VC−4VD)−VC−2VD=3010(-4V_C + 5V_D) - 3(5V_C - 4V_D) - V_C - 2V_D = 30 −40VC+50VD−15VC+12VD−VC−2VD=30-40V_C + 50V_D - 15V_C + 12V_D - V_C - 2V_D = 30 (−40−15−1)VC+(50+12−2)VD=30(-40 - 15 - 1)V_C + (50 + 12 - 2)V_D = 30 −56VC+60VD=30-56V_C + 60V_D = 30 Divide by 2: −28VC+30VD=15(7)-28V_C + 30V_D = 15 \quad (7)

Substitute into (2): −3(−4VC+5VD)+8(5VC−4VD)−2VC−VD=30-3(-4V_C + 5V_D) + 8(5V_C - 4V_D) - 2V_C - V_D = 30 12VC−15VD+40VC−32VD−2VC−VD=3012V_C - 15V_D + 40V_C - 32V_D - 2V_C - V_D = 30 (12+40−2)VC+(−15−32−1)VD=30(12 + 40 - 2)V_C + (-15 - 32 - 1)V_D = 30 50VC−48VD=3050V_C - 48V_D = 30 Divide by 2: 25VC−24VD=15(8)25V_C - 24V_D = 15 \quad (8)

Now solve the system of equations (7) and (8):

  1. −28VC+30VD=15-28V_C + 30V_D = 15
  2. 25VC−24VD=1525V_C - 24V_D = 15

Multiply (7) by 4 and (8) by 5 to eliminate V_D: 4×(−28VC+30VD)=4×15  ⟹  −112VC+120VD=604 \times (-28V_C + 30V_D) = 4 \times 15 \implies -112V_C + 120V_D = 60 5×(25VC−24VD)=5×15  ⟹  125VC−120VD=755 \times (25V_C - 24V_D) = 5 \times 15 \implies 125V_C - 120V_D = 75

Add the two new equations: (−112VC+120VD)+(125VC−120VD)=60+75(-112V_C + 120V_D) + (125V_C - 120V_D) = 60 + 75 13VC=13513V_C = 135 VC=13513 VV_C = \frac{135}{13} \text{ V}

Substitute V_C into (8) to find V_D: 25(13513)−24VD=1525\left(\frac{135}{13}\right) - 24V_D = 15 24VD=25×13513−1524V_D = \frac{25 \times 135}{13} - 15 24VD=3375−15×131324V_D = \frac{3375 - 15 \times 13}{13} 24VD=3375−1951324V_D = \frac{3375 - 195}{13} 24VD=31801324V_D = \frac{3180}{13} VD=318013×24=132.513=26526 VV_D = \frac{3180}{13 \times 24} = \frac{132.5}{13} = \frac{265}{26} \text{ V}

Now find V_A using (6): VA=−4VC+5VDV_A = -4V_C + 5V_D VA=−4(13513)+5(26526)V_A = -4\left(\frac{135}{13}\right) + 5\left(\frac{265}{26}\right) VA=−54013+132526V_A = -\frac{540}{13} + \frac{1325}{26} VA=−1080+132526V_A = \frac{-1080 + 1325}{26} VA=24526 VV_A = \frac{245}{26} \text{ V}

Finally, calculate the current in branch AD (I_AD). The resistance R_AD is 3Ω. IAD=VA−VDRADI_{AD} = \frac{V_A - V_D}{R_{AD}} IAD=24526−265263I_{AD} = \frac{\frac{245}{26} - \frac{265}{26}}{3} IAD=245−265263I_{AD} = \frac{\frac{245 - 265}{26}}{3} IAD=−20263I_{AD} = \frac{\frac{-20}{26}}{3} IAD=−1013×3I_{AD} = \frac{-10}{13 \times 3} IAD=−1039 AI_{AD} = -\frac{10}{39} \text{ A}

The negative sign indicates that the current flows from D to A, opposite to the assumed direction (A to D). The magnitude of the current is 1039\frac{10}{39} A.

The final answer is 1039A\boxed{\frac{10}{39} A}.

Explanation of the solution:

  1. Identify Nodes and Potentials: Assign potentials to all nodes in the circuit. Set one node (F) as reference (0V) and the connected battery terminal (E) as the battery voltage (30V).
  2. Apply KCL: Write Kirchhoff's Current Law equations for each unknown node (A, B, C, D). KCL states that the sum of currents leaving a node is zero. Express currents using Ohm's Law (I=V/RI = V/R).
  3. Formulate System of Equations: This results in a system of linear equations with the unknown node potentials as variables.
  4. Solve System of Equations: Solve the system of equations. In this case, a 4x4 system was reduced to a 2x2 system by substitution, then solved for V_C and V_D, and subsequently V_A and V_B.
  5. Calculate Desired Current: Once the potentials are known, calculate the current in the specified branch (AD) using Ohm's Law (IAD=(VA−VD)/RADI_{AD} = (V_A - V_D) / R_{AD}).

Answer:

The current in the branch AD is 1039A\frac{10}{39} A.