Question

A prism having an apex angle of $4^\circ$ and a refractive index of $1.50$ is located in front of a vertical plane mirror as shown. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is:

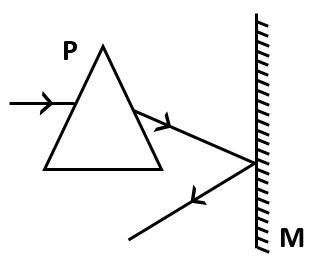
A. $4^\circ clockwise$
B. $178^\circ clockwise$
C. $2^\circ clockwise$
D. $8^\circ clockwise$

Answer 1

Use deviation formula to calculate deviation by prism. Then use the concept that the initial light ray and the normal of the mirror will be parallel to each other.

Formula used:
$\delta = \left( {\mu - 1} \right)A$
Where,
$A$ is apex angle
$\mu$ is refractive index
$\delta$ is the angle of deviation

Complete step by step answer:
It is given in the question that the prism has an apex angle of ${4^0}$
And the refractive index of $1.50$
This mirror is located in front of a mirror, M
Light ray is falling on the prism, horizontally.
We know that,
$\delta = \left( {\mu - 1} \right)A$
Where,
$A$ is apex angle
$\mu$ is refractive index
$\delta$ is the angle of deviation
Let, ${\delta _1}$ be the angle of deviation for the given prism when it refracts through the prism
Then we have
${\delta _1} = \left( {\mu - 1} \right)A$
Substitute the given values in the above equation. We get
${\delta _1} = (1.5 - 1)4$
$= 0.5 \times 4$
$\Rightarrow {\delta _1} = {2^0}$
This light ray will fall on the mirror and reflect.
Now observe the diagram

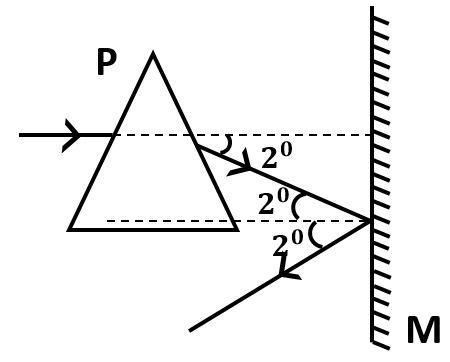
Since, the light ray was horizontal initially, it will be parallel to the normal to the mirror. Therefore, the angle of deviation will be equal to the angle of incidence.
And according to the law of reflection, the angle of incidence is equal to the angle or reflection.
Therefore, the deviation in the reflected ray from the mirror will be
${\delta _2} = {180^0} - 2 \times {2^0}$
$\Rightarrow {\delta _2} = {176^0}$
Now, the total deviation of the light ray will be the sum of the deviation from the prism and the deviation from the mirror.
Therefore, the total deviation of the light will be
$\delta = {\delta _1} + {\delta _2}$
$= {176^0} + {2^0}$
$\Rightarrow \delta = {178^0}$
Thus the total deviation is ${178^0}$.
From the diagram we can clearly observe that the deviation is in the clockwise direction.
Therefore, from the above explanation, the correct answer is, option (B) $178^\circ clockwise$

Note: In this equation, you need to understand how deviation would work in case of reflection. It was necessary to understand that the angle of deviation through prism is equal to the angle of incidence.