Question

A prism having an apex angle of ${4^ \circ }$ and a refractive index of $1.50$ is located in front of a vertical plane mirror as shown in the figure. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is?

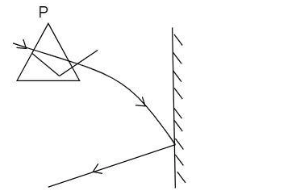
(A) ${4^ \circ }$ clockwise
(B) ${178^ \circ }$ clockwise
(C) ${2^ \circ }$ clockwise
(D) ${8^ \circ }$ clockwise

Answer 1

Use the formula of the angle of the prism, and substitute the refractive index of the prism and the apex angle of the prism in it to find the angle of the incidence. Subtract twice the incident angle by the ${180^ \circ }$ to find the angle of the reflection. Add both the angles to find the total angle.

Useful formula:
The formula of the prism is given by

${\delta _1} = \left( {\mu - 1} \right)A$

Where ${\delta _1}$ is the angle of the reflection of the prism, $\mu$ is the refractive index of the prism and $A$ is the apex of the prism.
Complete step by step solution:
The apex angle of the prism, $\theta = {4^ \circ }$
The refractive index of the prism, $n = 1.50$
The formula of the prism is taken,
${\delta _1} = \left( {\mu - 1} \right)A$
Substituting the known values in the above equation, we get
${\delta _1} = \left( {1.5 - 1} \right)4$
By simplification of the above equation, we get
${\delta _1} = {2^ \circ }$

As we know that the angle of incidence is equal to the angle of reflection, the angle of the incidence is obtained as ${2^ \circ }$ .
In the plane mirror, angle between the reflected ray and the angle of the incidence is obtained by ${\delta _2} = {180^ \circ } - 2i$
Substituting the angle of the incidence in the above equation, we get
${\delta _2} = {180^ \circ } - 2 \times 2 = {176^ \circ }$
Total angle of the reflection $= {\delta _1} + {\delta _2}$
$= 176 + 2 = {178^ \circ }$
Hence the angle of the reflection is obtained as ${178^ \circ }$ clockwise.

Thus the option (B) is correct.

Note: In the plane mirror, the reflecting surface provides the angle of the reflection which is equal to that of the angle of the incidence. This plane mirror has several applications like looking glasses, solar cookers and other scientific instruments etc.