Question

A potentiometer wire of length 10 m and resistance $30\text{ }\Omega$ is connected in series with a battery of emf 2.5 V, internal resistance 5 Ω, and an external resistance R. If the fall of potential along the potentiometer wire is $50\mu Vm{{m}^{-1}}$, then the value of R is found to be 23n Ω. What is n?

Answer 1

At first, we have to understand which system is given. Accordingly, write all given information and using standard formulas, calculate the required answer. Potential gradient is the ratio of potential difference and the length of potentiometer wire.

Complete answer:
Let I be the current in the circuit. E be emf, r is internal resistance and ${{R}_{s}}$ is the resistance of wire connected in series with battery.

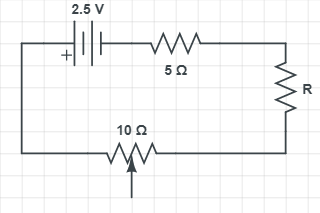
We know that the equation of emf,
$E=I(R+{{R}_{s}}+r)$
So, we can rearrange it to determine current I as
$I=\dfrac{E}{(R+{{R}_{s}}+r)}..........(1)$
The potential gradient k of the wire is
$k=\dfrac{I{{R}_{s}}}{L}......(2)$
where L is the length of the potentiometer wire.
Substituting value of I from equation (1) in equation (2) we get,
$k=\dfrac{E{{R}_{s}}}{(R+{{R}_{s}}+r)L}..........(3)$
Here it is given that, $L=10m,\text{ }E=2.5V,\text{ }r=5\Omega ,\text{ }{{R}_{s}}=30\Omega ,\text{ }k=50\mu Vm{{m}^{-1}}\text{, }R=23n\Omega$
Putting all these values in equation (3) we get,
$\dfrac{50\times {{10}^{-6}}}{{{10}^{-3}}}=\dfrac{2.5\times 30}{(R+30+5)10}$
Solving above equation and doing correct calculations we get,

& 50\times {{10}^{-6+3}}=\dfrac{2.5\times 3}{(R+35)} \\\ & \Rightarrow (R+35)=\dfrac{7.5}{50\times {{10}^{-3}}} \\\ & \Rightarrow (R+35)=0.15\times {{10}^{3}} \\\ & \Rightarrow R=150-35=115 \\\ \end{aligned}$$ But given R = 23n, so above equation can be written as, $$23n=115$$ Dividing throughout by 23, we get $$n=5$$ **Note:** Students must remember to convert the unit of potential gradient into SI unit because all the remaining values are in SI unit. Don’t forget to add internal resistance with the resistance R because they are in series with battery. Do calculations accurately otherwise it leads to wrong answers. Students sometimes just take E = IR and ignore internal resistance, this will lead to wrong answers.