Question

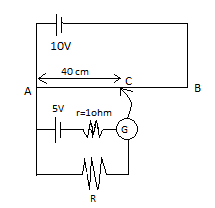
A potentiometer wire AB is 100cm long and has a total resistance of 10 ohms. If the galvanometer shows zero deflection at the position C, then find the value of unknown resistance R in ohms

Answer 1

First, find the potential gradient for the length AC from the potentiometer wire. The potentiometer is the decrease in potential per unit length given by the formula $\dfrac{V}{L}$, where V is the potential difference between two points, and L is the distance between two points. If the length of the wire is increased, then its potential gradient will decrease.

Complete step by step answer: Given
Length of wire AB$= 100cm$
The total resistance of the wire$r = 10\Omega$
Voltage$V = 10V$
So the potential gradient of the wire will be

$$x = \dfrac{V}{{{L_{AB}}}} \\\ = \dfrac{{10}}{{100}} \\\ = 0.1 \\\$$

Also the potential difference between point A and C will be

$${V_{AC}} = \dfrac{{{V_{AB}}}}{{{L_{AB}}}} \times {L_{AC}} - - (i) \\\ = 0.1 \times 40 \\\ = 4V \\\$$

It is given that when the pointer is at position C, then the galvanometer shows no deflection; hence we can say there is no current flow$i = 0$

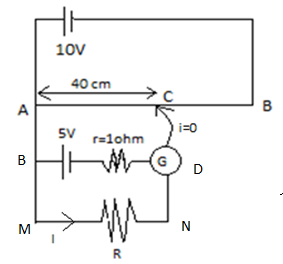
But a current I will flow through the resistor R, so the value of the current I will be

$$V = I\left( {R + r} \right) \\\ I = \dfrac{V}{{\left( {R + r} \right)}} \\\$$

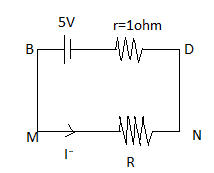
Now substitute the value of $V = 5V$and $r = 1ohm$
$I = \dfrac{5}{{\left( {R + 1} \right)}} - - (ii)$
Since the potential difference between point, A and C is${V_{AC}} = 4V$, hence this will be equal to the potential difference between BD and MN
${V_{AC}} = {V_{BD}} = {V_{MN}} = 4V$
Therefore we can say in terminal BD,

$${V_{BD}} = 5 - Ir \\\ 4 = 5 - I \\\ I = 1 - - (iii) \\\$$

Now b=substitute the value of I in the equation (ii) we get
$1 = \dfrac{5}{{\left( {R + 1} \right)}}$
Hence by solving, we get

$$\left( {R + 1} \right) = 5 \\\ R = 5 - 1 \\\ = 4\Omega \\\$$

Therefore the value of unknown resistance R $= 4\Omega$

Note: Students must note that when the potential across the scale is equal to the unknown applied EMF, then there will be no flow of current hence the galvanometer will show no deflections.