Question
Question: A potentiometer wire AB having length L and resistance \[12r\] is joined to a cell D of emf \[\varep...
A potentiometer wire AB having length L and resistance 12r is joined to a cell D of emf εand internal resistance r. A cell C having emf ε/2 and internal resistance 3r is connected. The length AJ at which the galvanometer was shown in fig. shows no deflection is:
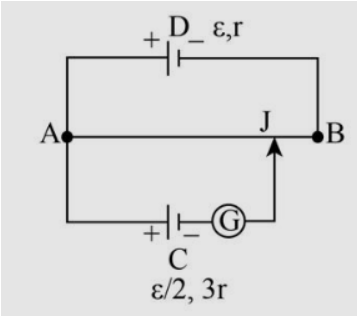
1. 125L
2. 2411L
3. 1211L
4. 2413L
Solution
The above problem can be resolved using the concept and the fundamentals of the potentiometer. In this problem, we are supposed to find the distance of a null point, from either end of the wire. For this, the basic approach is to calculate the potential gradient. Then after calculating the potential gradient of wire, one can go with the calculation of emf after reaching the null point. Then, at last, by making appropriate substitution of the numerically calculated values, we can obtain the necessary result of the null point distance.
Complete step by step answer:
Given:
The length of wire is, L.
The resistance of wire is, R1=12r.
The emf of cell D is, E1=ε.
The internal resistance of cell D is, R2=r.
The emf of cell C is, E2=2ε.
The internal resistance of cell C is, R3=3r.
We know the expression for the potential gradient as,
PG=I×LR1
Here, I is the magnitude of current through AB and its value is, ε/(R1+R2).
Solve by substituting the values as,
