Question

A potentiometer is connected across A and B and a balance is obtained at 64.0 cm. When the potentiometer lead at B is moved to C, a balance is found at 8.0 cm. If the potentiometer is now connected across B and C, a balance will be found at
A. 8.0 cm
B. 56.0 cm
C. 64.0 cm
D 72.0 cm

Answer 1

By using potentiometer we can measure the internal resistance of the cell or unknown emf of the cell. There will be voltage divided uniformly across the potentiometer wire and by balancing the cell at the length where the emf of the cell will be equal to potential difference across that portion of wire, we can find out unknown emf.

Complete step by step answer:
Resistance will be uniformly divided across the potentiometer wire. Current passing through the potentiometer wire is constant. Resistance is proportional to the length of the potentiometer wire. Since current is constant throughout the potentiometer wire and resistance is proportional to its length, potential difference also will be proportional to its length. Diagram for the potentiometer is given below.

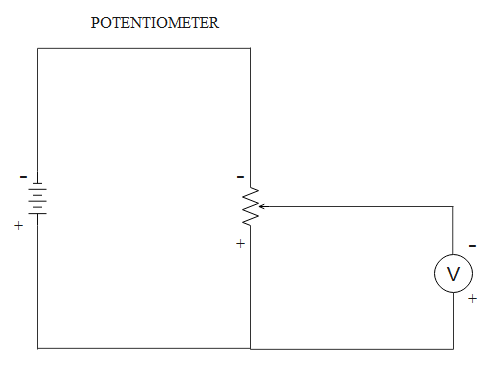
In the above diagram, the terminal where positive sign is marked, is at higher potential and the terminal where negative sign is marked, is at lower potential.
When we connect any external battery of unknown emf to the potentiometer the current keeps on flowing from battery to potentiometer as long as the voltage across the potentiometer wire leads will be equal to the emf of that unknown battery. That point is called the balance point.
Potential difference is given by $V = \phi l$
Where $\phi$ is constant.
In the first case
${V_1} = \phi {l_1}$
$\Rightarrow {V_A} - {V_B} = \phi (64)$ …eq1
In the second case
${V_2} = \phi {l_2}$
$\Rightarrow {V_A} - {V_C} = \phi (8)$ …eq2
If we subtract equation 2 from equation 1 we will get
\eqalign{ & \Rightarrow \left( {{V_A} - {V_B}} \right) - \left( {{V_A} - {V_C}} \right) = \phi (64) - \phi (8) \cr & \therefore {V_C} - {V_B} = \phi (56) \cr}
Hence if a potentiometer is connected across B and C, balance would be found at 56cm.

So, the correct answer is “Option B”.

Note:
At the balance point, by knowing the length of the distance between two leads we can find out the emf of the unknown battery, because the length is proportional to the potential difference across those two points. If constant is not known then we can compare the unknown emf with the known emf.