Question

A potential barrier of 0.5 V exists across a p-n junction (i) If the depletion region is $5\times {{10}^{-7}}$ m wide. What is the average intensity of the electric field in the region? (ii) An electron with speed $5\times {{10}^{5}}m/s$ approaches the p-n junction from the n-side with what speed will it enter the p-side?

Answer 1

Hint: speed of electron will decrease because when electron enters the p – side from n – side, it crosses a barrier and so its speed decreases. To calculate the final velocity of an electron in the p- side, just apply kinetic energy balance or do conservation of energy.

Complete step by step answer:

Average intensity of the electric field
given data,
d = $5\times {{10}^{-7}}$m
$\begin{aligned} & \overrightarrow{E}=\dfrac{v}{d} \\\ & \overrightarrow{E}=\dfrac{0.5V}{5\times {{10}^{-7}}} \\\ & \overrightarrow{E}={{10}^{6}}v/m \\\ \end{aligned}$
Here, $\overrightarrow{E}$= average intensity of the electric field
V = potential
d = depletion width

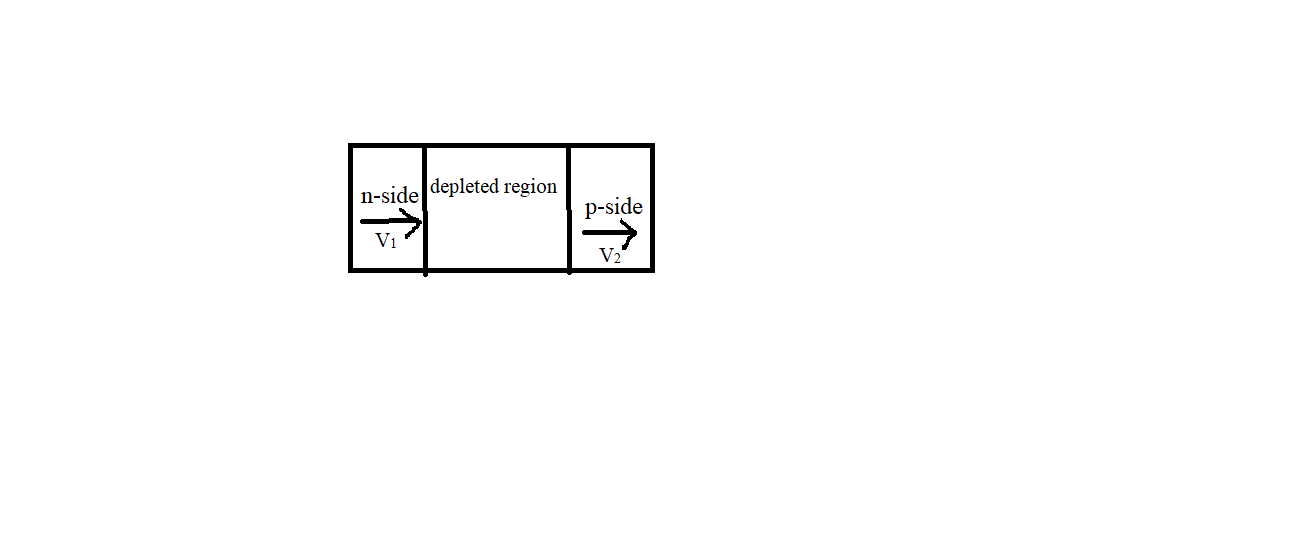
Given data

Speed of electron $5\times {{10}^{5}}m/s$ in n-side
Mass of electron =$9.1\times {{10}^{-31}}$ kg

Applying conservation of energy

Kinetic energy before entering = ev + Kinetic energy after reaching p-side

& \dfrac{1}{2}mv_{1}^{2}=ev+\dfrac{1}{2}mv_{2}^{2} \\\ & \dfrac{1}{2}(9.1\times {{10}^{-31}}){{(5\times {{10}^{5}})}^{2}}=(1.5\times {{10}^{-19}})0.5+\dfrac{1}{2}(9.1\times {{10}^{-31}})v_{2}^{2} \\\ & \dfrac{1}{2}(9.1\times {{10}^{-31}})v_{2}^{2}=\dfrac{1}{2}(9.1\times {{10}^{-31}}){{(5\times {{10}^{5}})}^{2}}-(1.5\times {{10}^{-19}})0.5 \\\ & v_{2}^{2}=7.2\times {{10}^{10}} \\\ & {{v}_{2}}=\sqrt{7.2\times {{10}^{10}}} \\\ & {{v}_{2}}=2.68\times {{10}^{5}}m/s \\\ \end{aligned}$$ Note: Conservation of energy, conservation of momentum and conservation of mass are very important laws in physics. Always apply this whenever required. Conservation of mass is called continuity equation and conservation of energy is known as Bernoulli’s principle.