Question

A pot maker rotates a pot making wheel of radius 3 m by applying a force of 200 N tangentially. If wheel completes exactly $\dfrac{3}{2}$ revolutions, work done by him is:
A. 5654.86 J
B. 4321.32 J
C. 4197.5 J
D. 1884.96 J

Answer 1

We are given a situation where a pot maker makes pots. The radius of the wheel and the applied force is given to us. To find the total work done, we need to find the torque acting on the wheel due to the applied force and angle of rotation for the given number of revolutions. We can solve for the work done by applying these values in the equation.

Formula used:
Torque,
$\tau =r\times F$
Work done,
$W=\int{\tau d\theta }$

Complete answer:

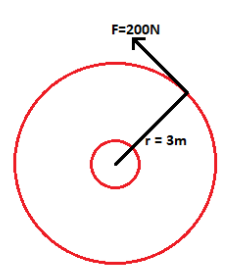
In the above figure we have a pot wheel.
In the question it is said that the radius of the wheel is 3 m and it is also said a force of 200 N is applied tangentially to the wheel.
Therefore we have,
Force, F = 200 m
Radius, r = 3m
When the wheel spins due to the applied force, the wheel experiences a torque.
This torque can be given as,
$\tau =r\times F$
$\begin{aligned} & \tau =3\times 200 \\\ & \tau =600N \\\ \end{aligned}$
We need to find the work done by him when he completes a total of $\dfrac{3}{2}$ revolutions.
We know work done is expressed as,
$W=\int{\tau d\theta }$
Here we know that torque is constant.
Therefore, work done
$W=\tau \Delta \theta$
We know that ‘$\theta$’ is the angle of rotation.
Here the angle of rotation is the angle rotated to complete $\dfrac{3}{2}$ revolutions.
For $\dfrac{3}{2}$ revolutions, $\theta =\dfrac{3}{2}\times 2\pi =3\pi \pi$
Therefore,
$\begin{aligned} & W=600\times 3\times 3.14 \\\ & W=5654.86J \\\ \end{aligned}$
Therefore the work done to complete $\dfrac{3}{2}$ revolutions is 5654.86 J

Hence the correct answer is option A.

Note:
We know that the equation to find torque is,
$\tau =r\times F$
In this equation, the force should be perpendicular to the distance or radius.
In the given case it is said that the force is applied tangentially. From this we can infer that the angle between radius and force is ${{90}^{o}}$, i.e. radius and force are perpendicular to each other.