Question
Question: A positively charged particle of charge ‘q’ enters in a uniform magnetic field ‘B’ directed inwards ...
A positively charged particle of charge ‘q’ enters in a uniform magnetic field ‘B’ directed inwards and it is deflected a distance y0 after travelling a distance x0as shown in the figure. Then the magnitude of linear momentum of the particle is
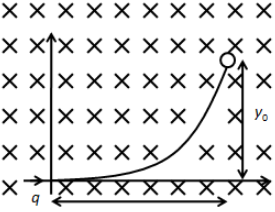
A. 2qBx0
B. 2qB(y0x02+x0)
C. 2y0qB(x02+y02)
D. 2qB(y0+y0x02)
Solution
Find the radius of the circular path using Pythagoras theorem. The necessary centripetal force required for the circular motion of the particle is provided by the magnetic force. The linear momentum of the particle is the product of its mass and velocity.
Formula used:
Magnetic force, FB=qvB,
where, q is the charge, B is the magnetic field and v is the velocity.
Centripetal force, FC=rmv2,
where, m is the mass and r is the radius of the circular motion.
Complete step by step answer:
We know that when the charge particle enters a magnetic field, it is deflected due to the magnetic force acting on it to change its direction. In the uniform magnetic field, the particle will deflect at each point so that the particle will follow a circular path.Let us find the radius of the circular path using the following figure.
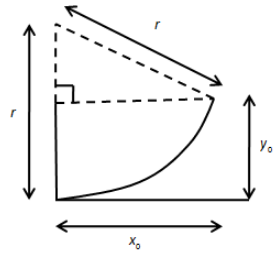
Using the Pythagoras theorem in the above triangle, we get,
r2=(r−y0)2+x02
⇒r2=r2−2ry0+y02+x02
⇒2ry0=y02+x02
⇒r=2y0y02+x02
⇒r=21(y0+y0x02) …… (1)
The necessary centripetal force required for the circular motion of the particle is provided by the magnetic force. Therefore, we can write,
rmv2=qvB
⇒rmv=qB
⇒mv=qBr …… (2)
Here, m is the mass, v is the velocity, r is the radius of the circular motion, q is the charge and B is the magnetic field.
We know that the linear momentum of the particle is given as,
p=mv
From equation (2), we can write the linear momentum of the particle as,
p=qBr
Using equation (1) in the above equation, we get,
p=qB(21(y0+y0x02))
⇒p=2qB(y0+y0x02)
So, the correct answer is option D.
Note: When the distance y0 becomes equal to radius r, the distance x0 also equals the radius r and therefore, the linear momentum at this position is equal to p=qBr. We have given that the particle enters in only uniform magnetic field and electric field is not applied in this region. In the case of an electric field, the force on the particle will be the contribution from both electric field and magnetic field.
