Question

A positively charged particle of 2.0 C moves upward into an area where both a magnetic field and an electric field are acting. The magnetic field has a magnitude of $4.0 \times {10^4}\;T$ and the electric field has a magnitude of 0.1 N/C. At what velocity must the particle be moving if it is not deflected when it enters this area.

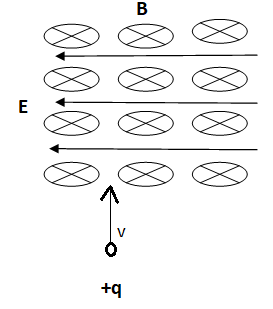
A) $4.0 \times {10^{ - 3}}\;m/s$
B) $125m/s$
C) $250m/s$
D) $500m/s$

Answer 1

A particle follows a straight line path if the net resultant of all the forces acting on that body is acting on that line. So if we want a particle to get un-deviated from its path we must have to balance all the forces acting on it in such a way that the net force is zero on the particle.

Complete step by step answer:
If we have to pass the particle un-deviated then there should be net force equal to zero on the particle.
In that case both electric force and magnetic force are normalized to each other.
Force on charged particles due to electric fields should be equal to force on charged particles by magnetic force.
Force on charged particle due to electric field = $qE$; $E = 0.1N/C$
$\Rightarrow {F_{electric}} = qE$………. Eq(1)
Force on charged particle by magnetic force = $qvB$; $B = 4.0 \times {10^4}T$
$\Rightarrow {F_{magnetic}} = qvB$……….Eq(2)
Force on charged particle due to electric field = Force on charged particle by magnetic force.
From eq(1) and eq(2), we get
$\Rightarrow {F_{electric}} = {F_{magnetic}}$
$\Rightarrow qE = qvB$
Solving for the velocity, we get
$\Rightarrow v = \dfrac{{qE}}{{qB}}$
$\Rightarrow v = \dfrac{E}{B}$ where $E = 0.1N/C$ & $B = 4.0 \times {10^4}T$
Putting all the values we get
$\Rightarrow v = \dfrac{{0.1}}{{4 \times {{10}^{ - 4}}}}m/s$
Simplifying the equation we get
$\Rightarrow v = 250m/s$
This means the velocity must be $v = 250m/s$ of the particle if it is not deflected when it enters this area.
Since the value of the velocity is $v = 250m/s$.

Hence option ( C ) is the correct answer.

Note:
Both electric field and magnetic field affect the trajectory of charged particles, but in qualitatively different ways.
The force on a charged particle due to an electric field is directed parallel to the electric field vector in the case of a positive charge, and antiparallel in the case of a negative charge.
An electric field may do work on a charged particle, while a magnetic field does not work.