Question

A positive charge $Q = 50 \mu C$ is located in the xy plane at a point having at a point having position vector $\vec{r_{o}} = 2 \hat{i} + 3 \hat{j}$ m where $\hat{i}$ and $\hat{j}$ are unit vectors in the positive directions of X and Y, axis respectively. Find:
a) The electric intensity vector and its magnitude at a point having coordinates $(8m, -5m)$
b) Work done by the external agent in transporting a charge $q = 10 \mu C$ from $(8m, 6m)$ to the point $(4m, 3m)$.

Answer 1

The electric field E at any point may be described as the electric force F applied per unit positive electric charge q at that location. If the charge is double as significant, the resultant force is multiplied, but the electric field E measure remains the same at any given point. The electric field depends on the reference charge, not on the test charge. The work done by the outer force is equivalent to the change in the electrostatic potential energy in the outer field. The difference in the potential energy of a charge q when moving from point A to point B is the work done by an outside force in shifting the charge.

Complete step-by-step solution:
Given: $Q = 50 \mu C$

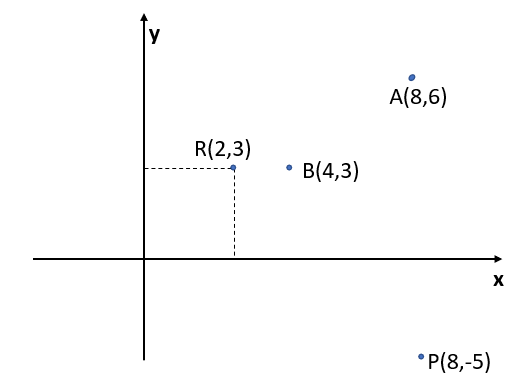
a) We have to calculate the electric field at point P due to the charge being placed on point R.
Electric field is given by:
$E = \dfrac{kQ\vec{r}}{|\vec{r}^{3}|}$
r is the position vector between P and R points.
$\vec{r} = 8 \hat{i} – 5 \hat{j} – ( 2 \hat{i} + 3 \hat{j})$
$\implies \vec{r} = 6 \hat{i} – 8 \hat{j}$
$|\vec{r}| = \sqrt{6^{2} + (-8)^{2}}$
It gives,
$r = 10 m$
Now, find electric field at P,
$E = \dfrac{9 \times 10^{9} \times 50 \times 10^{-6} \times (6 \hat{i} – 8 \hat{j})}{1000}$
$E = 450 (6 \hat{i} – 8 \hat{j}) NC{-1}$
b) We have to find the work done in transporting a charge $q = 10 \mu C$ from A $(8m, 6m)$ to the point B $(4m, 3m)$.
Work done is equal to change in electrostatic potential energy.
$W = U _{B} – U_{A}$
$W= \dfrac{kQq}{r_{2}} - \dfrac{kQq}{r_{1}}$
$q = 10 \mu C$
$r_{1}$ is the distance between P and B.
$r_{2}$ is the distance between P and A.
$r_{1} = \sqrt{(4-2)^{2} + (3-3)^{2}} \implies r_{1} = 2m$
$r_{2} = \sqrt{(8-2)^{2} + (6-3)^{2}} \implies r_{2} = \sqrt{45}m$
$W= kQq\left( \dfrac{1 }{r_{2}} - \dfrac{1}{r_{1}} \right)$
$W= 9 \times 10^{9} \times 50 \times 10^{-6} \times 10 \times 10^{-6} \left( \dfrac{1 }{2} - \dfrac{1}{\sqrt{45}} \right)$
$W = 1.57 joules$

Note: The difference in potential energy is proportionate to the charge. Its sign depends whether the charge is negative or positive. We explain the potential difference as the potential energy difference distributed by the charge. As in gravity, the zero potential energy and the zero potential are not uniquely determined.