Question

A position dependent force F acting on a particle and its force-position curve is shown in figure. Work done on the particle when its displacement 0 to 5 m is:

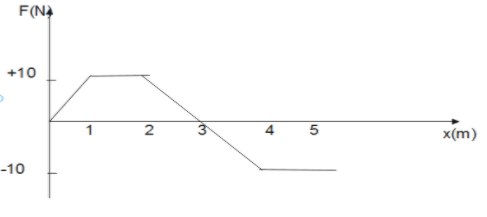
1. 35 J
2. 25 J
3. 45 J
4. 5 J

Answer 1

Work done on an object depends on the amount of force F causing the work, the displacement d experienced by the object. Also, work done is given by the area under the F-x curve. S.I unit of work is Joule (J).
Total area under the given curve can be calculated by dividing the curve in small areas and adding them.

Formula used:
Work done= area under F-x curve.
Area of triangle${A_T} = \dfrac{1}{2} \times base \times height$
Area of rectangle${A_R} = length \times breadth$

Complete answer:
We know that, Work done on an object depends on the amount of force F causing the work, the displacement d experienced by the object.
Work done = area under F-x curve.
Or, W= Area

From above figure:
\eqalign{ & W = {A_1} + {A_2} + {A_3} - ({A_4} + {A_5}) \cr & \Rightarrow W = \left[ {\dfrac{1}{2} \times 1 \times 10} \right] + [1 \times 10] + \left[ {\dfrac{1}{2} \times 1 \times 10} \right] - \left[ {\dfrac{1}{2} \times 1 \times 10 + 10 \times 1} \right] \cr & \Rightarrow W = 5 + 10 + 5 - (5 + 10) \cr & \therefore W = 5J \cr}
Therefore, option 4) is correct i.e., work done on the particle, when the displacement is 0 to 5 m is 5 Joule.

Additional information:
Work done can also be given by $W = Fd\cos \theta$, here $\theta$ is the angle between the force vector F and the displacement vector d.
If the angle between the force vector and the displacement d is zero, then the work done is maximum.
If the angle between the force vector and displacement d is ${90^ \circ }$, the work done is zero.
Force is push or pull upon an object’s interaction with another object. From Newton’s second law force F is given by the product of mass m and acceleration a. Acceleration is the rate of change of the velocity of an object with respect to time. Acceleration is a vector quantity.
Deceleration is when the speed or velocity decreases. It can also be defined as the acceleration which is opposite to the velocity.

Note:
Work done on an object depends on the amount of force F causing the work, the displacement d experienced by the object. So, if there is no displacement then the work done upon the object is zero. Also, in work when the force and the displacement are perpendicular to each other we do not have to do any work.